Page 56 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

4. Tema : Eşlik Ve Benzerlik

Paralel Çizme Temel Orantı Teoremi

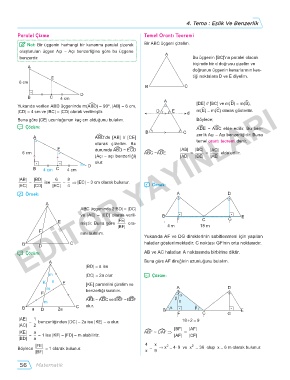
{ Not: Bir üçgenin herhangi bir kenarına paralel çizerek Bir ABC üçgeni çizelim.
oluşturulan üçgen Açı - Açı benzerliğine göre bu üçgene A
benzerdir. Bu üçgenin [BC]'na paralel olacak
biçimde bir d doğrusu çizelim ve
A
doğrunun üçgenin kenarlarının kes-
E tiği noktalara D ve E diyelim.
6 cm
B C
D
B C 4 cm
A [DE] // [BC] ve m(ëD) = m(ëB),
EDİTÖR YAYINLARI
Yukarıda verilen ABD üçgeninde m(AéBD) = 90º, |AB| = 6 cm,
|CD| = 4 cm ve |BC| = |CD| olarak verilmiştir. D E d m(ëE) = m(ëC) olarak gösterilir.
Buna göre |CE| uzunluğunun kaç cm olduğunu bulalım. Böylece;
̚ Çözüm: A¿DE ~ A¿BC elde edilir. Bu ben-
B C
A A¿BD’de [AB] // [CE] zerlik Açı - Açı benzerliğidir. Buna
olarak çizelim. Bu temel orantı teoremi denir.
E durumda A¿BD ~ E¿CD |AB| |BC| |AC|
6 cm A¿BC ~A¿DE = = elde edilir.
(Açı - açı benzerliği) |AD| |DE| |AE|
olur.
D
B 4 cm C 4 cm

|AB| = |BD| ise 6 = 8 ⇒ |EC| = 3 cm olarak bulunur.
|EC| |CD| |EC| 4 ̛ Örnek:
̛ Örnek: A D
A
ABC üçgeninde 2|BD| = |DC|
ve |AE| = |EC| olarak veril- B E
E miştir. Buna göre |FE| ora- F C G
|BF| 4 m 18 m
F nını bulalım.
Yukarıda AF ve DG direklerinin sabitlenmesi için yapılan
B D C halatlar gösterilmektedir. C noktası GF’nin orta noktasıdır.
̚ Çözüm: AB ve AC halatları A noktasında birbirine diktir.
A Buna göre AF direğinin uzunluğunu bulalım.
|BD| = a ise

m |DC| = 2a olur. ̚ Çözüm:
K a E [KE] paralelini çizelim ve
m A D
F benzerliği kuralım. α

m A¿KE ~ A¿DC ve E¿KF ~ B¿DF β x
B a D 2a C olur. B α β E
F C G
|AE| = 1 benzerliğinden |DC| = 2a ise |KE| = a olur. 18 2÷ = 9
|AC| 2 |BF| |AF|
|KE| = a = 1 ise |KF| = |FD| = m alabiliriz. A¿BF ~ C¿AF ⇒ =
|BD| a |AF| |CF|
|FE| 4 x 2 2
Böylece = 1 olarak bulunur. = ⇒ x = 4 . 9 ve x = 36 olup x = 6 m olarak bulunur.
|BF| x 9

56 Matematik