Page 52 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

4. Tema : Eşlik Ve Benzerlik

ÜÇGENLERİN BENZER OLMA ŞARTLARI
● Karşılıklı kenar uzunlukları orantılı ve karşılıklı açıları eş olan üçgenler benzer üçgenlerdir.

● A¿BC ile D¿EF benzer üçgenler ise A¿BC ~ D¿EF şeklinde gösterilir.
● Benzer üçgenlerin karşılıklı kenarlarının uzunlukları oranına benzerlik oranı denir.

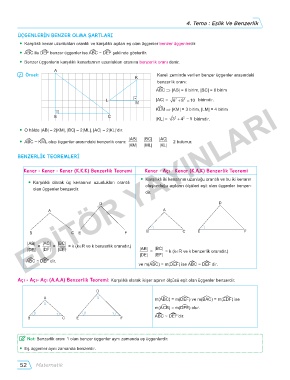
A
̛ Örnek: K Kareli zeminde verilen benzer üçgenler arasındaki
benzerlik oranı:

A¿BC ⇒ |AB| = 6 birim, |BC| = 8 birim
L M |AC| = 6 2 + 2 = 8 10 birimdir.
EDİTÖR YAYINLARI
K¿LM ⇒ |KM| = 3 birim, |LM| = 4 birim
B C |KL| = 3 + 2 4 = 2 5 birimdir.

● O hâlde |AB| = 2|KM|, |BC| = 2|ML|, |AC| = 2|KL|’dır.
|AB| |BC| |AC|
● A¿BC ~ K¿ML olup üçgenler arasındaki benzerlik oranı: = = = 2 bulunur.
|KM| |ML| |KL|

BENZERLİK TEOREMLERİ

Kenar - Kenar - Kenar (K.K.K) Benzerlik Teoremi Kenar - Açı - Kenar (K.A.K) Benzerlik Teoremi

● Karşılıklı iki kenarının uzunluğu orantılı ve bu iki kenarın
● Karşılıklı olarak üç kenarının uzunlukları orantılı oluşturduğu açıların ölçüleri eşit olan üçgenler benzer-
olan üçgenler benzerdir.
dir.

D D
A A

B C E F B C E F
|AB| = |AC| = |BC| = k (k∈R ve k benzerlik oranıdır.)
|DE| |DF| |EF| |AB| = |BC| = k (k∈R ve k benzerlik oranıdır.)
|DE| |EF|
A¿BC ~ D¿EF dir.
ve m(AéBC) = m(DéEF) ise A¿BC ~ D¿EF dir.

Açı - Açı- Açı (A.A.A) Benzerlik Teoremi: Karşılıklı olarak ikişer açının ölçüsü eşit olan üçgenler benzerdir.

D
A α m(AéBC) = m(DéEF) ve m(BéAC) = m(EéDF) ise
α
m(AéCB) = m(DéFE) olur.
β γ β γ
B C E F A¿BC ~ D¿EF’dir.

{ Not: Benzerlik oranı 1 olan benzer üçgenler aynı zamanda eş üçgenlerdir.

● Eş üçgenler aynı zamanda benzerdir.

52 Matematik