Page 98 - 10. SINIF MATEMATİK FAVORİ DEFTERİM

ETKİNLİK DEFTERİ 5. ÜNİTE: DÖRTGENLER VE ÇOKGENLER

7. Paralelkenar

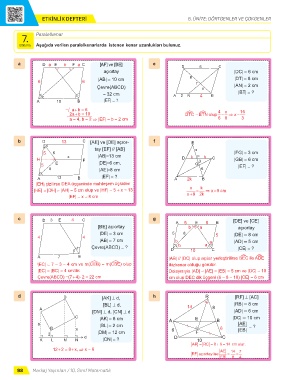
Etkinlik Aşağıda verilen paralelkenarlarda istenen kenar uzunlukları bulunuz.

a D a E b F a C [AF] ve [BE] e D 6 C
açıortay |DC| = 6 cm

6 6 |AB| = 10 cm 8 T |DT| = 8 cm
Çevre(ABCD) x |AN| = 2 cm
= 32 cm A 2 N 4 B |BT| = ?
A 10 B |EF| = ?
- a + b = 6 4 x 16
2a + b = 10 DTCÿ  BTN olupÿ =  x =
a = 4, b = 2  |EF| = b = 2 cm 68 3

b D 13 C [AE] ve [DE] açıor- f E
tay [EF] // [AB] x
5 6 |AB|=13 cm |FG| = 3 cm
H x F D k F k C |GB| = 6 cm
3
5 E |DE|=6 cm, G |EF| = ?
8 |AE|=8 cm 6
A 13 B |EF| = ? A 2k B
|EH| çizilirse DEA üçgeninde muhteşem üçlüden
|HE| = |DH| = |AH| = 5 cm olup ve |HF| = 5 + x = 13 x = k  x =9 cm
|EF| = x = 8 cm x +9 2k

c D 3 E 4 C g 5 5 [DE] ve [CE]
[BE] açıortay A b E a B açıortay
|DE| = 3 cm 5 8 5 |DE| = 8 cm
4 4
|AB| = 7 cm b a |AD| = 5 cm
Çevre(ABCD) = ? D b 10 a C |CE| = ?

A 7 B |AB| // |DC| olup açılar yerleştirilirse B¿EC ile A¿DE
|EC| = 7 - 3 = 4 cm ve m(CéEB) = m(CéBE) olup ikizkenar olduğu görülür.
|EC| = |BC| = 4 cm'dir. Dolayısıyla |AD| = |AE| = |EB| = 5 cm ve |DC| = 10
Çevre(ABCD) =(7 + 4) . 2 = 22 cm cm olup DEC dik üçgeni (6 - 8 - 10) |CE| = 6 cm

d D [AK] ⊥ d, h R [RF] ⊥ [AC]

[BL] ⊥ d, |RB| = 8 cm
A 14 8
[DM] ⊥ d, [CN] ⊥ d |AD| = 6 cm
C |AK| = 8 cm A E B |DC| = 10 cm
8 |BL| = 2 cm |AE|
B x 6 6 |EB| = ?
2 |DM| = 12 cm F
K L M N d |CN| = ? D 10 C
AR = RC = 8 6+ = 14 cm olur.
12 + 2 = 8 + x,  x = 6 AE
RF açýortay ise = 14 = 7
EB 8 4

98 Markaj Yayınları / 10. Sınıf Matematik