Page 92 - 10. SINIF MATEMATİK FAVORİ DEFTERİM

ETKİNLİK DEFTERİ 5. ÜNİTE: DÖRTGENLER VE ÇOKGENLER

2. Dörtgenlerde Kenar ve Açı Özellikleri

Etkinlik Aşağıda verilen çokgenlerde istenen değerleri bulunuz.

a d D C

D
C E
64 o
72 o F 10 o
A x

B A B

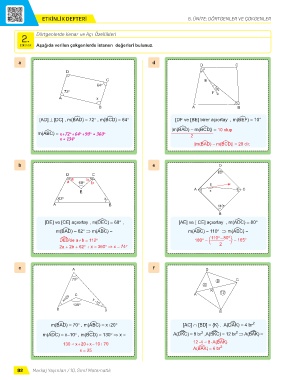
[AD] ⊥ [DC] , m(BéAD) = 72° , m(BéCD) = 64° [DF ve [BE] birer açıortay , m(BéEF) = 10°
|m(BéAD) - m(BéCD)| = 10 olup
m(AéBC) = x + 72 + 64 + 90 = 360 2
x = 134
|m(BéAD) - m(BéCD)| = 20 dir.

b e D
80 o
D C
a a 68 o b b E

A C
E x
62 o x
A B 110 o

B
[DE] ve [CE] açıortay , m(DéEC) = 68° , [AE] ve [ CE] açıortay , m(AéDC) = 80°
m(BéAD) = 62° ⇒ m(AéBC) = m(AéBC) = 110° ⇒ m(AéEC) =
110- 80
DÿEB'de a + b = 112 180 - � � = 165°
2a + 2b + 62 + x = 360  x = 74 2

c A f D

70 O 8 C
4
K 12
x+20 C A
130 O x -10
B D B

m(BéAD) = 70° , m(AéBC) = x+20° [AC] ∩ [BD] = {K} , A(D¿AK) = 4 br 2
2
2
m(AéDC) = x-10° , m(BéCD) = 130° ⇒ x = A(D¿KC) = 8 br ,A(B¿KC) = 12 br ⇒ A(B¿AK) =
12 . 4 = 8 . A(BÿAK)
130 = x + 20 + x - 10 + 70 2
x = 25 A(BÿAK) = 6 br

92 Markaj Yayınları / 10. Sınıf Matematik