Page 106 - 10. SINIF MATEMATİK FAVORİ DEFTERİM

ETKİNLİK DEFTERİ 5. ÜNİTE: DÖRTGENLER VE ÇOKGENLER

13. Dikdörtgen

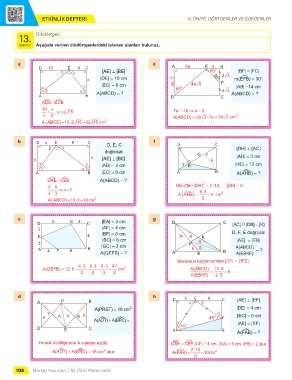
Etkinlik Aşağıda verilen dikdörtgenlerdeki istenen alanları bulunuz.

a e A 6a E a
D 10 E 6 C B
β α [AE]  [BE] 60° añ3 |BF| = |FC|
x |DE| = 10 cm 2añ3 30° F m(EéFB) = 30°

α β |EC| = 6 cm 60° 4añ3 |AB| =14 cm
β α añ3
A B A(ABCD) = ? D C A(ABCD) = ?
ÿ
ÿ
ADB ECB
10 x = 7a = 14  a = 2
= , x 2 15
x 6 A(ABCD) = 2añ3 . 7a = 56ñ3 cm 2
A (ABCD )= 16 ⋅ =2 15 32 15 cm 2

b D x E 9 C f
β α D, E, C D C [DH] ⊥ [AC]
doğrusal
3 [AE] ⊥ [BE] 12 |AH| = 3 cm
3 6
α β 3 |HC| = 12 cm
β α |AD| = 3 cm H
A B |EC| = 9 cm A B A(A¿HB) = ?
ÿ
ÿ
DAE CEB A(ABCD) = ?
.
2
39  x1 Öklid'ten |DH| = 3 12, |DH| = 6
=
=
( )
x3 A AHB =ÿ 63 ⋅ = 9 cm 2
⋅=
A (ABCD )=10 3 30cm 2 2
c g
D 9 G 3 C |EA| = 3 cm D C [AC] ∩ [DB] = {K}
3 |AF| = 4 cm D, F, E doğrusal
|BF| = 8 cm
E 6 |BC| = 6 cm 2k S K |AE| = |EB|
3 |GC| = 3 cm F S
A 4 F 8 B A(GEFB) = ? A k E S B A(ABCD) = ?
A(EBKF)
Menelaus bağıntısından |DF| = 2|FE|
⋅
43 93 ⋅ ⋅ 63 87
⋅
A(GEFB) 12 6= ⋅− − − = cm 2 A(ABCD) 12 S
2 2 2 2 A(EBKF) = 2 S ⋅ = 6

d h 4 E 6
A P B D α β C [AE] ⊥ [EF]
A(PRST) = 18 cm 2 |DE| = 4 cm
T A α
A A A R 45° F |EC| = 6 cm
A(A¿DT) + A(B¿RC) =
β |AE| = |EF|
D S C A 45° B A(F¿AB) = ?

Yamuk özelliğinden A alanları eşittir. DÿAE ≡ CÿEF |CF| = 4 cm, |DA| = 6 cm |FB| = 2 olur.
⋅
2
A(A¿DT) + A(B¿RC) = 18 cm olur. A(FAB)=ÿ 2 10 = 10cm 2
2

106 Markaj Yayınları / 10. Sınıf Matematik