Page 109 - 10. SINIF MATEMATİK FAVORİ DEFTERİM

5. ÜNİTE: DÖRTGENLER VE ÇOKGENLER ETKİNLİK DEFTERİ

16. Deltoid

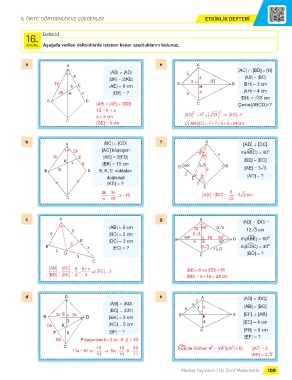
Etkinlik Aşağıda verilen deltoidlerde istenen kenar uzunluklarını bulunuz.

a A e A
|AB| = |AD| 5 [AC] ∩ [BD] = {H}
6 |BK| = 2|KE| 4 |AB| = |BC|
12 A A B 3 ò33 D |BH| = 3 cm
k E |AE| = 6 cm H
2k K x |DE| = ? 5 4 |AH| = 4 cm
|DH| = ò33 cm
B D
|AB| = |AE| + |ED| C Çevre(ABCD)=?
12 = 6 + x 2 A 2
A
x = 6 cm = AD 2 + 4 ( 33 ) ⇒ = AD 7
C |DE| = 6 cm Ç (ABCD ) = +++=7755 24cm

b A |BC| = |CD| f A [AD] ⊥ [DC]

2k [AC] köşegen 30° m(AéBC) = 60°
3k E |AE| = 2|ED| 30° x
K x k A A |BK| = 15 cm |BE| = |EC|

B 15 D B, K, E noktaları B 60º 3ñ3 6 D |AE| = 3ñ3
3
doğrusal E 60° |AD| = ?
|KE| = ? 3
C
2k 3k AD = DC = 6 = 3 2 cm
C x = 15 x 10= 2

c A g A |AD| = |DC| =
|AB| = 6 cm 30° 60° 12ñ3
6 12ñ3 cm
6 |BD| = 2 cm 6ñ3 30° o
E |DC| = 3 cm B 60º 6 E 18 30º D m(AéBE) = 60
2 o
B x |EC| = ? 6ñ3 m(EéDC) = 30
2 12ñ3
D C |BD| = ?
3
C
AB = AC = 6 6x  EC = 3 |BE| = 6 ve |ED| = 18
+
=
BD DC 2 3 |BD| = 6 + 18 = 24 cm

d A h A |AD| = |DC|
|AB| = |AD| F 2 |AB| = |BC|
|BC| = |CD| 6 x 4
B 3k E 3k D |EK| = 3 cm B E D [EF]  [AB]
3 4 |EC| = 4 cm
6a K |KC| = 5 cm
F 5 |BF| = ? C |FB| = 6 cm
.
5a Pisagordan k = 2 dir. 5 2 = 10 |EF| = ?
C 10 10 60 AÿEB'de öklitten 4 = |AF|(|AF| + 6) |AF| = 2
2
11a 10 a= = → 6a = 6 ⋅=
11 11 11 |EF| = 2ñ3

Markaj Yayınları / 10. Sınıf Matematik 109