Page 31 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

2. Tema : Nicelikler Ve Değişimler

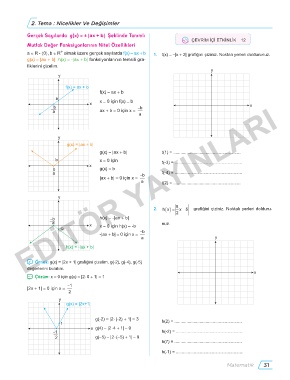
Gerçek Sayılarda g(x) = ± |ax + b| Şeklinde Tanımlı
ÇEVRİM İÇİ ETKİNLİK - 12
Mutlak Değer Fonksiyonlarının Nitel Özellikleri
+
a ∈ R - {0}, b ∈ R olmak üzere gerçek sayılarda f(x) = ax + b 1. t(x) = -|x + 2| grafiğini çiziniz. Noktalı yerleri doldurunuz.
g(x) = |ax + b| h(x) = -|ax + b| fonksiyonlarının temsili gra-
fiklerini çizelim.
y
y

f(x) = ax + b
f(x) = ax + b
b
EDİTÖR YAYINLARI
x x = 0 için f(x) = b x
− b -b
a ax + b = 0 için x =
a

y
g(x) = |ax + b|
g(x) = |ax + b| t(1) = ........................................................
b x = 0 için t(-3) = ........................................................
x
− b g(x) = b
a -b t(-4) = ........................................................
|ax + b| = 0 için x =
a t(2) = ........................................................

y

( )
−
2. hx = 5 x 5 grafiğini çiziniz. Noktalı yerleri dolduru-
2
− b h(x) = -|ax + b|
a x nuz.
-b x = 0 için h(x) = -b
-|ax + b| = 0 için x = -b
a y

h(x) = -|ax + b|

̛ Örnek: g(x) = |2x + 1| grafiğini çizelim. g(-2), g(-4), g(-5)
değerlerini bulalım.
x
̚ Çözüm: x = 0 için g(x) = |2 . 0 + 1| = 1

-1
|2x + 1| = 0 için x =
2
y
g(x) = |2x+1|

.
g(-2) = |2 (-2) + 1| = 3 h(2) = ��������������������������������������������������������
1
x g(4) = |2 . 4 + 1| = 9
− 1 h(-2) = ��������������������������������������������������������
2 g(-5) = |2 . (-5) + 1| = 9
h(7) = ��������������������������������������������������������

h(-1) = ��������������������������������������������������������

Matematik 31