Page 26 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

2. Tema : Nicelikler Ve Değişimler

f(x) = x fonksiyonu R → R tanımlı olduğu için maksimum ve
minimum noktalarından bahsedilemez. ÇEVRİM İÇİ ETKİNLİK - 9
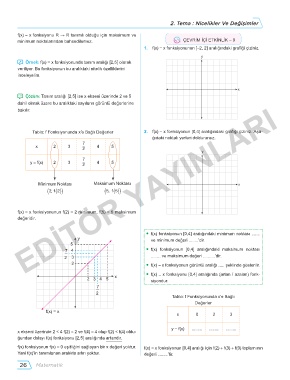
1. f(x) = x fonksiyonunun [-2, 2] aralığındaki grafiği çiziniz.
y
̛ Örnek: f(x) = x fonksiyonunda tanım aralığı [2,5] olarak
veriliyor. Bu fonksiyonun bu aralıktaki nitelik özelliklerini
inceleyelim.

x
̚ Çözüm: Tanım aralığı [2,5] ise x ekseni üzerinde 2 ve 5
EDİTÖR YAYINLARI
dahil olmak üzere bu aralıktaki sayıların görüntü değerlerine
bakılır.

Tablo: f Fonksiyonunda x’e Bağlı Değerler 2. f(x) = x fonksiyonun [0,4] aralığındaki grafiği çiziniz. Aşa-
ğıdaki noktalı yerleri doldurunuz.
7
x 2 3 2 4 5
y
7
y = f(x) 2 3 2 4 5

Minimum Noktası Maksimum Noktası x
( ))
( ))
( 2, f 2 ( 5, f 5

f(x) = x fonksiyonunun f(2) = 2 minimum, f(5) = 5 maksimum
değeridir.

● f(x) fonksiyonun [0,4] aralığındaki minimum noktası .......
y ve minimum değeri ........’dir.
5
7 4 ● f(x) fonksiyonun [0,4] aralığındaki maksimum noktası
2 3 ........ ve maksimum değeri ..........’dir.
2 ● f(x) = x fonksiyonun görüntü aralığı ..... şeklinde gösterilir.
● f(x) = x fonksiyonu [0,4] aralığında (artan / azalan) fonk-
2 3 4 5 x siyondur.
7
2
Tablo: f Fonksiyonunda x’e Bağlı
Değerler
f(x) = x
x 0 2 3

y = f(x) ��������� ��������� ���������
x ekseni üzerinde 2 < 4 f(2) = 2 ve f(4) = 4 olup f(2) < f(4) oldu-
ğundan dolayı f(x) fonksiyonu [2,5] aralığında artandır.
f(x) fonksiyonun f(x) = 0 eşitliğini sağlayan bir x değeri yoktur. f(x) = x fonksiyonun [0,4] aralığı için f(2) + f(3) + f(0) toplamının
Yani f(x)’in tanımlanan aralıkta sıfırı yoktur. değeri .........’tir.

26 Matematik