Page 21 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

1. Tema : Sayılar

GERÇEK SA
GERÇEK SAYILARIN İŞLEM ÖZELLİKLERİYILARIN İŞLEM ÖZELLİKLERİ
ÖNERME KAVRAMI

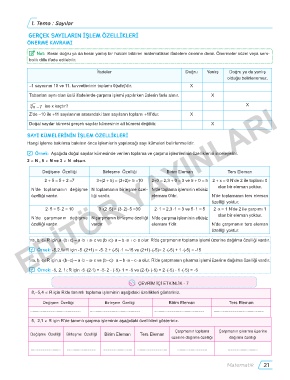
{ Not: Kesin doğru ya da kesin yanlış bir hüküm bildiren matematiksel ifadelere önerme denir. Önermeler sözel veya sem-
bolik dille ifade edilebilir.

İfadeler Doğru Yanlış Doğru ya da yanlış
olduğu belirlenemez.
-1 sayısının 10 ve 11. kuvvetlerinin toplamı 0(sıfır)’dır. X
Tabanları aynı olan üslü ifadelerde çarpma işlemi yapılırken üslerin farkı alınır. X
EDİTÖR YAYINLARI
3 x = 7 ise x kaçtır? X
Z’de -10 ile +11 sayılarının arasındaki tam sayıların toplamı +10’dur. X
Doğal sayılar kümesi gerçek sayılar kümesinin alt kümesi değildir. X

SAYI KÜMELERİNİN İŞLEM ÖZELLİKLERİ
Hangi işleme bakılırsa bakılsın önce işlemlerin yapılacağı sayı kümeleri belirlenmelidir.

̛ Örnek: Aşağıda doğal sayılar kümesinde verilen toplama ve çarpma işlemlerinin özelliklerini inceleyelim.
2 ∈ N , 5 ∈ N ve 3 ∈ N olsun.

Değişme Özelliği Birleşme Özelliği Birim Eleman Ters Eleman
2 + 5 = 5 + 2 =7 3+(2 + 5) = (3+2)+ 5 =10 2+0 = 2,3 + 0 = 3 ve 5 + 0 = 5 2 + x = 0 N’de 2 ile toplamı 0
olan bir eleman yoktur.
N’de toplamanın değişme N toplamanın birleşme özel- N’de toplama işleminin etkisiz
özelliği vardır. liği vardır. elemanı 0’dır. N’de toplamanın ters eleman
özelliği yoktur.
2 . 5 = 5 . 2 = 10 3 . (2 . 5) = (3 . 2) . 5 =30 2 . 1 = 2,3 . 1 = 3 ve 5 . 1 = 5 2 . x = 1 N’de 2 ile çarpımı 1
olan bir eleman yoktur.
N’de çarpmanın değişme N çarpmanın birleşme özelliği N’de çarpma işleminin etkisiz
özelliği vardır. vardır. elemanı 1’dir. N’de çarpmanın ters eleman
özelliği yoktur.

∀a, b, c∈R için,a . (b+c) = a . b + a . c ve (b+c) . a = b . a + c . a olur. R’de çarpmanın toplama işlemi üzerine dağılma özelliği vardır.
̛ Örnek: -5,2,1∈R için -5 . (2+1) = -5 . 2 + (-5) . 1 =-15 ve (2+1) . (-5)= 2 . (-5) + 1 . (-5) = -15

∀a, b, c∈R için,a . (b-c) = a . b - a . c ve (b-c) . a = b . a - c . a olur. R’de çarpmanın çıkarma işlemi üzerine dağılma özelliği vardır.

̛ Örnek: -5, 2, 1∈R için -5 . (2-1) = -5 . 2 - (-5) . 1 = -5 ve (2-1) . (-5) = 2 . (-5) - 1 . (-5) = -5

ÇEVRİM İÇİ ETKİNLİK - 7
8,-5,4 ∈ R için R’de tanımlı toplama işleminin aşağıdaki özellikleri gösteriniz.

Değişme Özelliği Birleşme Özelliği Birim Eleman Ters Eleman
�������������������������������������������� �������������������������������������������� �������������������������������������������� ��������������������������������������������

5,-2,1 ∈ R için R’de tanımlı çarpma işleminin aşağıdaki özellikleri gösteriniz.
Çarpmanın toplama Çarpmanın çıkarma üzerine
Değişme Özelliği Birleşme Özelliği Birim Eleman Ters Eleman
üzerine dağılma özelliği dağılma özelliği

�������������������������� �������������������������� �������������������������� �������������������������� �������������������������� ��������������������������

Matematik 21