Page 22 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

1. Tema : Sayılar

Matematikte Sembolik Dil Özdeşliklerin Cebirsel ve Geometrik Temsilleri
İki veya daha fazla önermeyi birlikte ifade edebilmek için man- ÖNEMLİ ÖZDEŞLİKLER
tık bağlaçlarından faydalanılır. 1. İki sayının toplamının karesi

Niceleyiciler (a + b) = a + 2ab + b 2
2
2

Sembol ∃ ∀ 2. İki sayının farkının karesi
2
2
Bazı (a - b) = a - 2ab + b 2
Anlamı Her 3. İki kare farkı
(En az bir)
2
2
a - b = (a - b) (a + b)
Niceleyiciler
EDİTÖR YAYINLARI

Sembol ∧ ∨ ∨ ⇒ ⇔ a + b
ancak 2
2
2
Anlamı ve veya ya da ise ve a + b a ab (a + b) = (a + b) . (a + b) = a + 2ab + b 2
ancak ab b 2
̛ Örnek:Aşağıda verilen önermeleri sembolik dil kullana-
rak yazalım. Örnekleri inceleyelim.
a - b b ( − ab ) = 2 2 −a   − + − + 2 b(ab) b(ab) b 
a - b (a - b) 2 b(a - b) = 2 − a   − 2 + −ab b 2 + b 2 ab b 
Her a, b pozitif gerçek sayıları için a, b’den küçük ise b’nin a - b
a’dan çıkarılması ile elde edilen sonuç sıfırdan küçüktür. b b(a - b) b b a 2 −  =  − 2 2ab b 
2
a - b b = 2 − a + 2ab b bulunur.
2
+
∀ a, b ∈ R , için a ˂ b ⇒ a-b ˂ 0 olur.
4, 5∈ R için 4 ˂ 5 ⇒ 4-5 ˂ 0 -1 ˂ 0
a
b b a
a b =
Sıfırdan farklı her a gerçek sayısı için a ile b sayısının çarpı- a - b
mının 1 olmasını sağlayan en az bir b gerçek sayısı vardır. a b
2
2
a - b = (a + b) . (a - b)
∀ a ∈ R, a ≠ 0 için ∃ b ∈ R vardır. Öyle ki a . b =1
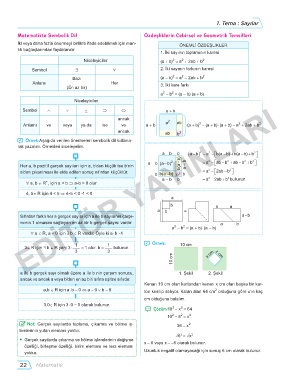
3∈ R için ∃ b ∈ R yani 3 . 1 = 1 olur. b = 1 bulunur. ̛ Örnek: 10 cm
3 3
10 cm x cm x cm

a ile b gerçek sayı olmak üzere a ile b nin çarpım sonucu, 1. Şekil 2. Şekil
ancak ve ancak a veya b’den en az biri sıfıra eşitse sıfırdır.
Kenarı 10 cm olan kartondan kenarı x cm olan başka bir kar-
a,b ∈ R için a . b = 0 ⇔ a = 0 ∨ b = 0 ton kesilip atılıyor. Kalan alan 64 cm olduğuna göre x’in kaç
2
cm olduğunu bulalım.
3,0∈ R için 3 . 0 = 0 olarak bulunur.
2
2
̚ Çözüm: 10 - x = 64
2
2
10 - 8 = x 2
{ Not: Gerçek sayılarda toplama, çıkarma ve bölme iş- 36 = x 2
lemlerinin yutan elemanı yoktur.
2
ò6 = òx 2
● Gerçek sayılarda çıkarma ve bölme işlemlerinin değişme x = 6 veya x = -6 olarak bulunur.

özelliği, birleşme özelliği, birim elemanı ve ters elemanı
yoktur. Uzunluk negatif olamayacağı için sonuç 6 cm olarak bulunur.
22 Matematik