Page 27 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

2. Tema : Nicelikler Ve Değişimler

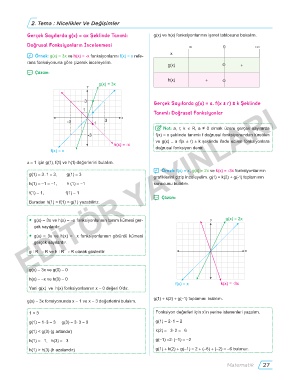
Gerçek Sayılarda g(x) = ax Şeklinde Tanımlı g(x) ve h(x) fonksiyonlarının işaret tablosuna bakalım.

Doğrusal Fonksiyonların İncelenmesi -∞ 0 +∞
x
̛ Örnek: g(x) = 3x ve h(x) = -x fonksiyonlarını f(x) = x refe-
rans fonksiyonuna göre çizerek inceleyelim.
g(x) - +
̚ Çözüm:
h(x) + -
y g(x) = 3x

3 Gerçek Sayılarda g(x) = a . f(x ± r) ± k Şeklinde
EDİTÖR YAYINLARI
1
Tanımlı Doğrusal Fonksiyonlar
x
-3 1 3
{ Not: a, r, k ∈ R, a ≠ 0 olmak üzere gerçek sayılarda
-3 f(x) = x şeklinde tanımlı f doğrusal fonksiyonundan türetilen
ve g(x) = a . f(x ± r) ± k şeklinde ifade edilen fonksiyonlara
h(x) = -x
f(x) = x doğrusal fonksiyon denir.

x = 1 için g(1), f(1) ve h(1) değerlerini bulalım.
̛ Örnek: f(x) = x, g(x) = 2x ve k(x) = -3x fonksiyonlarının
g(1) = 3 � 1 = 3, g(1) = 3
grafiklerini çizip inceleyelim. g(1) + k(2) + g(-1) toplamının
h(1) = -1 = -1, h (1) = -1 sonucunu bulalım.
f(1) = 1, f(1) = 1
̚ Çözüm:
Buradan h(1) < f(1) < g(1) yazabiliriz.

● g(x) = 3x ve h(x) = -x fonksiyonlarının tanım kümesi ger- y g(x) = 2x
çek sayılardır.
● g(x) = 3x ve h(x) = -x fonksiyonlarının görüntü kümesi
gerçek sayılardır.

g : R → R ve h : R → R olarak gösterilir. x

g(x) = 3x ve g(0) = 0

h(x) = -x ve h(0) = 0
f(x) = x k(x) = -3x
Yani g(x) ve h(x) fonksiyonlarının x = 0 değeri 0’dır.

g(1) + k(2) + g(-1) toplamını bulalım.
g(x) = 3x fonsiyonunda x = 1 ve x = 3 değerlerini bulalım.

1 < 3 Fonksiyon değerleri için x’in yerine istenenleri yazalım.
g(1) = 1 . 3 = 3 g(3) = 3 . 3 = 9 g(1) = 2 . 1 = 2
g(1) < g(3) (g artandır) k(2) = -3 . 2 = -6

h(1) = -1, h(3) = -3 g(-1) =2 . (-1) = -2
h(1) > h(3) (h azalandır) g(1) + k(2) + g(-1) = 2 + (-6) + (-2) = -6 bulunur.

Matematik 27