Page 28 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

2. Tema : Nicelikler Ve Değişimler

Gerçek Sayılarda a∈R Olmak Üzere g(x) = a y

Şeklinde Tanımlı Doğrusal Fonksiyonların
İncelenmesi

1
{ Not: f : R → R, f(x) = ax + b ve b∈R olmak üzere -1 0 x
a = 0 için f(x) = b şeklinde tanımlı fonsiyonlara sabit fonksiyon
denir.

1
EDİTÖR YAYINLARI
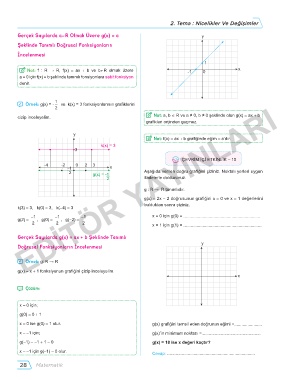
̛ Örnek: g(x) = - ve k(x) = 3 fonksiyonlarının grafiklerini
2
cizip inceleyelim. { Not: a, b ∈ R ve a ≠ 0, b ≠ 0 şeklinde olan g(x) = ax + b
grafikleri orijinden geçmez.

y
{ Not: f(x) = ax + b grafiğinde eğim = a’dır.
k(x) = 3
3

ÇEVRİM İÇİ ETKİNLİK - 10
-4 -2 0 2 3
1 − x
2 g(x) = -1 Aşağıda verilen doğru grafiğini çiziniz. Noktalı yerleri uygun
2 ifadelerle doldurunuz.
g : R → R tanımlıdır.

g(x) = 2x - 2 doğrusunun grafiğini x = 0 ve x = 1 değerlerini
bulduktan sonra çiziniz.
k(3) = 3, k(0) = 3, k(-4) = 3

-1 -1 -1 x = 0 için g(0) = ................................................................
g(2) = , g(0) = , g(-2) =
2 2 2 x = 1 için g(1) = .................................................................

Gerçek Sayılarda g(x) = ax + b Şeklinde Tanımlı
y
Doğrusal Fonksiyonların İncelenmesi

̛ Örnek: g: R → R

g(x) = x + 1 fonksiyonun grafiğini çizip inceleyelim.
x

̚ Çözüm:

x = 0 için;
g(0) = 0 + 1
x = 0 ise g(0) = 1 olur. g(x) grafiğini temsil eden doğrunun eğimi =.......................

x = -1 için; g(x)’in minimum noktası =.................................................
g(-1) = -1 + 1 = 0 g(x) = 18 ise x değeri kaçtır?
x = -1 için g(-1) = 0 olur. Cevap: �������������������������������������������������������������������������

28 Matematik