Page 32 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

2. Tema : Nicelikler Ve Değişimler

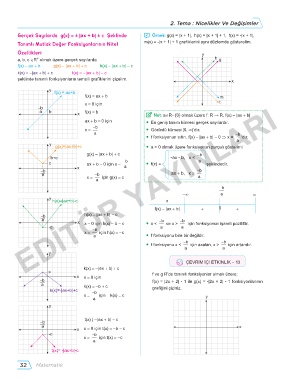
Gerçek Sayılarda g(x) = ± |ax + b| ± c Şeklinde ̛ Örnek: g(x) = |x + 1|, h(x) = |x + 1| + 1, t(x) = -|x + 1|,
Tanımlı Mutlak Değer Fonksiyonlarının Nitel m(x) = -|x + 1| + 1 grafiklerini aynı düzlemde gösterelim.

Özellikleri y
+
a, b, c ∈R olmak üzere gerçek sayılarda h g

f(x) = ax + b g(x) = |ax + b| + c h(x) = |ax + b| - c
k(x) = -|ax + b| + c t(x) = -|ax + b| - c
şeklinde tanımlı fonksiyonların temsili grafiklerini çizelim. x
y
f(x) = ax+b
f(x) = ax + b m
EDİTÖR YAYINLARI
x = 0 için t
− b
a b x f(x) = b { Not: a∈R- {0} olmak üzere f: R → R, f(x) = |ax + b|

ax + b = 0 için ● En geniş tanım kümesi gerçek sayılardır.
-b
x = ● Görüntü kümesi [0, ∞)’dır.
a -b
● f fonksiyonun sıfırı, f(x) = |ax + b| = 0 ⇒ x = ’dır.
a
y g(x)=|ax+b|+c ● a > 0 olmak üzere fonksiyonun parçalı gösterimi
g(x) = |ax + b| + c -b
b+c -ax - b, x <
c ax + b = 0 için x = -b ● f(x) = a şeklindedir.
x a
− b -b
a -b ax + b, x ≥
x = için g(x) = c a
a
-b
-∞ a ∞
y
h(x)=|ax+b|-c x
f(x) = |ax + b| + 0 +
− b h(x) = |ax + b| - c
a -b -b
x x = 0 için h(x) = b - c ● x < ve x > için fonksiyonun işareti pozitiftir.
-c -b a a
x = için h(x) = -c
a ● f fonksiyonu bire bir değildir.
-b -b
● f fonksiyonu x < için azalan, x > için artandır.
a a
y
ÇEVRİM İÇİ ETKİNLİK - 13
k(x) = -|ax + b| + c
c f ve g R’de tanımlı fonksiyonlar olmak üzere;
x x = 0 için
− b f(x) = |2x + 2| - 1 ile g(x) = -|2x + 2| - 1 fonksiyonlarının
a k(x) = -b + c
k(x)=-|ax+b|+c -b grafiğini çiziniz.
x = için k(x) = c y
a
y

t(x) ) -|ax + b| - c
− b
a x x = 0 için t(x) = -b - c x
-c -b
x = için t(x) = -c
a
t(x)= -|ax+b|-c

32 Matematik