Page 34 - 9. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

2. Tema : Nicelikler Ve Değişimler

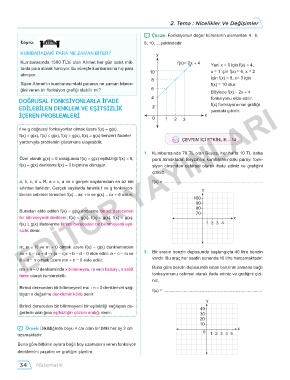
̚ Çözüm: Fonksiyonun değer kümesinin elemanları 4 , 6,
Köprü: 8, 10, ....şeklindedir

KUMBARADAKİ PARA NE ZAMAN BİTER? y
Kumbarasında 1500 TL’si olan Ahmet her gün sabit mik- f(x)= 2x + 4 Yani x = 0 için f(x) = 4,
tarda para alarak harcıyor. Bu süreçte kumbarasına hiç para x = 1 için f(x) = 6, x = 2
atmıyor. 10
8 için f(x) = 8, x= 3 için
Sizce Ahmet'in kumbarasındaki paranın ne zaman bitece- f(x) = 10 olur.
ğini veren bir fonksiyon grafiği olabilir mi? 6 Böylece f(x) = 2x + 4
4 fonksiyonu elde edilir.
DOĞRUSAL FONKS f(x) fonksiyonunun grafiği
DOĞRUSAL FONKSİYONLARLA İFADE İYONLARLA İFADE
Buradan elde edilen f(x) = g(x) ifadesine birinci dereceden YAYINLARI
ED 2 yandaki gibidir.
EDİLEBİLEN DENKLEM VE EŞİTSİZLİK İLEBİLEN DENKLEM VE EŞİTSİZLİK
İÇEREN PROBLEMLER 0 1 2 3 x
İÇEREN PROBLEMLERİİ
f ve g doğrusal fonksiyonlar olmak üzere f(x) = g(x),
f(x) < g(x), f(x) ≤ g(x), f(x) > g(x), f(x) ≥ g(x) benzeri ifadeler
yardımıyla problemin çözümüne ulaşılabilir. ÇEVRİM İÇİ ETKİNLİK - 14

1. Kumbarasında 70 TL olan Beyza, her hafta 10 TL daha
Özel olarak g(x) = 0 olduğunda f(x) < g(x) eşitsizliği f(x) < 0, para atmaktadır. Beyza’nın kumbarasındaki parayı fonk-
f(x) = g(x) denklemi f(x) = 0 biçimine dönüşür. siyon cinsinden cebirsel olarak ifade ediniz ve grafiğini
çiziniz.
a, b, c, d ∈ R, a ≠ c, a ve c gerçek sayılarından en az biri f(x) = ..................................................................................
EDİTÖR
sıfırdan farklıdır. Gerçek sayılarda tanımlı f ve g fonksiyon- y
larının cebirsel temsilleri f(x) = ax + b ve g(x) = cx + d olsun.
100
90
80
70
bir bilinmeyenli denklem; f(x) < g(x), f(x) ≤ g(x), f(x) > g(x), x
f(x) ≥ g(x) ifadelerine birinci dereceden bir bilinmeyenli eşit- 1 2 3 4
sizlik denir.

m, n ∈ R ve m ≠ 0 olmak üzere f(x) = g(x) denkleminden
ax + b = cx + d ⇒ (a - c)x + b - d = 0 elde edilir. a - c = m ve 2. Bir aracın benzin deposunda başlangıçta 40 litre benzin
b - d = n olmak üzere mx + n = 0 elde edilir. vardır. Bu araç her saatin sonunda 10 litre harcamaktadır.
mx + n = 0 denkleminde x bilinmeyen, m ve n katsayı, n sabit Buna göre benzin deposunda kalan benzinin zamana bağlı
terim olarak isimlendirilir. fonksiyonunu cebirsel olarak ifade ediniz ve grafiğini çizi-
niz.
Birinci dereceden bir bilinmeyenli mx + n = 0 denklemini sağ- f(x) = ..................................................................................
layan x değerine denklemin kökü denir.
y
Birinci dereceden bir bilinmeyenli bir eşitsizliği sağlayan de- 40
ğerlerin aralığına eşitsizliğin çözüm aralığı denir. 30
20
10
̛ Örnek: Dikildiğinde boyu 4 cm olan bir bitki her ay 2 cm 0 x
uzamaktadır. 1 2 3 4 5

Buna göre bitkinin aylara bağlı boy uzamasını veren fonksiyon
denklemini yazalım ve grafiğini çizelim.

34 Matematik