Page 44 - Geometri Çalışma Yaprakları - Giriş Yayınları

TYT GEOMETRİ 4. BÖLÜM: ÇEMBERDE AÇI

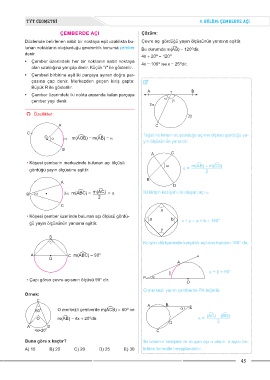
ÇEMBERDE AÇI Çözüm:

Düzlemde belirlenen sabit bir noktaya eşit uzaklıkta bu- Çevre açı gördüğü yayın ölçüsünün yarısına eşittir.
lunan noktaların oluşturduğu geometrik konuma çember Bu durumda m(AïB) = 120 dir.
o
denir. 4x + 20 = 120 o
o
• Çember üzerindeki her bir noktanın sabit noktaya 4x = 100 ise x = 25 dir.
o
o

olan uzaklığına yarıçap denir. Küçük "r" ile gösterilir.
• Çemberi birbirine eşit iki parçaya ayıran doğru par-
çasına çap denir. Merkezden geçen kiriş çaptır. {
Büyük R ile gösterilir.
A T B
• Çember üzerindeki iki nokta arasında kalan parçaya α
çember yayı denir. β
2α

Ÿ Özellikler: 2β

A C
C
O α α m(AùOB) = m(AïB) = a Teğet ile kirişin oluşturduğu açının ölçüsü gördüğü ya-
yın ölçüsünün yarısıdır.

B
A C
• Köşesi çemberin merkezinde bulunan açı ölçüsü α m(AïB) + m(CïD)
gördüğü yayın ölçüsüne eşittir. a = 2

B
A
D
B α 2α m(AùBC) = m(AïC) = a İki kirişin kesişimi ile oluşan açı a
2
C
x
• Köşesi çember üzerinde bulunan açı ölçüsü gördü- a b
ğü yayın ölçüsünün yarısına eşittir. x + y = a + b = 180°
y
B
Kirişler dörtgeninde karşılıklı açıların toplamı 180° dir.

A C m(AéBC) = 90°
O
A

β a + β = 90°
• Çapı gören çevre açısının ölçüsü 90° dir. P α O

O merkezli yarım çemberde PA teğettir.
Örnek:
C
A B E
o
60 o O merkezli çemberde m(AéCB) = 60 ve α
o
O m(AïB) = 4x + 20 dir. a = (AïC) - (BïD)
D 2
A B
4x+20 o C

Buna göre x kaçtır? İki kesenin kesişimi ile oluşan açı a olsun. a açısı be-
A) 15 B) 20 C) 20 D) 25 E) 30 lirtilen formülle hesaplanabilir.

43