Page 62 - Geometri Çalışma Yaprakları - Giriş Yayınları
P. 62
TYT GEOMETRİ 6. BÖLÜM: NOKTANIN ANALİTİĞİ
NOKTANIN ANALİTİĞİ K noktasının uzaklığı 2ñ2 birim
Başlangıç noktası aynı olan iki doğrunun dik kesişmesi L noktasının uzaklığı ò10 birim
ile oluşturduğu sisteme koordinat sistemi denir.
C noktası orijin ise;
y (ordinat)
y (ordinat)
. . K noktasının uzaklığı 5 birim (3-4-5 üçgeni)
II. Bölge . . . . I. Bölge L noktasının uzaklığı 5 birimdir.
x<0 3 3 x>0
y>0 2 2 y>0 Orijin C noktasıdır.
1 1
. . .
. . .
. . . -3 -3 -2 -2 -1 -1 O O 1 1 22 3 3 . . . x (apsis) { İki Nokta Arasındaki Uzaklık
x (apsis)
-1 -1
III. Bölge -2 -2 IV. Bölge ABC üçgeninde pisagor bağıntısından
x<0 -3 -3 x>0 y y
y<0 . . . . y<0 AB = 2 (x - x ) + 2 (y - y ) 2
. . B B 2 1 2 1
y y
2 2
y
y −y−y 1 1
2 2
y y AB = (x - 2 x ) + 1 2 (y - 2 y ) 2
1
x
• Koordinat sisteminde yatay eksene x ekseni (apsis), 1 1 A A x −x−x C C
1 1
2 2
dikey eksene y ekseni (ordinat) denir. O O x x 1 1 x x 2 2 x x
• Koordinat sisteminde 4 bölge vardır.
• Koordinat sisteminde 1. noktanın bileşeni x eksenin- Doğru Parçasının Orta Noktasının Koordinatları
den, 2. bileşeni y ekseninden alınır. Nokta A(x, y)
şeklindedir. y y
• Doğruların kesişim noktasına orijin (başlangıç nok- y y 2 2 B B (x
(x ,y ),y )
tası) denir. C C 2 2 2 2
C 1 2 , y +y 2 x +x
1
A A
Örnek: y y 1 1 (x 2 2
(x ,y ),y )
1 1 1 1
O O x x 1 1 x x 2 2 x x
Örnek:
K
E D Köşeleri A(3,4), B(6,5) ve C(9,3) olan ABC üçgeninin
B A ağırlık merkezinin koordinatları aşağıdakilerden han-
gisidir?
C L
A) (3,4) B) (4,4) C) (5,4) D) (6,4) E) (4,6)
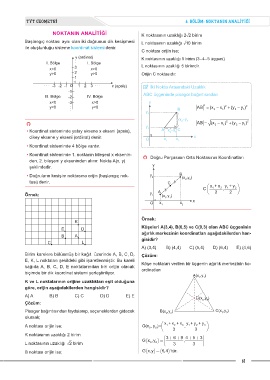
Birim karelere bölünmüş bir kağıt üzerinde A, B, C, D, Çözüm:
E, K, L noktaları şekildeki gibi işaretlenmiştir. Bu kareli Köşe noktaları verilen bir üçgenin ağırlık merkezinin ko-
kağıda A, B, C, D, E noktalarından biri orijin olacak ordinatları
biçimde bir dik koordinat sistemi yerleştiriliyor.
A(x ,y )
1 1
K ve L noktalarının orijine uzaklıkları eşit olduğuna
göre, orijin aşağıdakilerden hangisidir?
A) A B) B C) C D) D E) E G(x ,y )
Çözüm: 0 0
Pisagor bağıntısından faydalanıp, seçeneklerden gidecek B(x ,y ) C(x ,y )
2 2 3 3
olursak;
y +y +y x +x +x
A noktası orijin ise; G(x , y 0 = ) 1 2 3 , 1 2 3
0
3 3
K noktasının uzaklığı 2 birim 3 + + 9 4 ++ 3
6
5
G (x ,y ) = ,
L noktasının uzaklığı ñ2 birim 0 0 3 3
B noktası orijin ise; G (x,y ) (6,4 tür.= )'
61