Page 58 - Geometri Çalışma Yaprakları - Giriş Yayınları
P. 58
TYT GEOMETRİ 5. BÖLÜM: KONİ
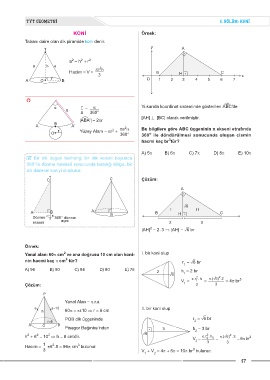
KONİ Örnek:
Tabanı daire olan dik piramide koni denir.
y
T A
2
2
a = h + r 2
a h a 2
Hacim = V = πr h B H C
r 3 O 5 7 x
A O B 1 2 3 4 6
α r a Yukarıda koordinat sisteminde gösterilen A¿BC'de
a a = 360°
[AH] ⊥ [BC] olarak verilmiştir.
|AùBA'| = 2πr
A B A' 2
2
r Yüzey Alanı = πr + πa a Bu bilgilere göre ABC üçgeninin x ekseni etrafında
O 360° 360 ile döndürülmesi sonucunda oluşan cismin
o
3
hacmi kaç br tür?
A) 5π B) 6π C) 7π D) 8π E) 10π
{ Bir dik üçgen herhangi bir dik kenarı boyunca
360°lik dönme hareketi sonucunda taradığı bölge, bir
dik dairesel koniyi oluşturur.
C C Çözüm:
A
ñ6
A B A B B H C
Dönme 360° dönme
ekseni açısı 2 3
2
.
|AH| = 2 3 ⇒ |AH| = ñ6 br
Örnek:
2
Yanal alanı 60π cm ve ana doğrusu 10 cm olan koni- I. bir koni olup
3
nin hacmi kaç π cm tür? r = ñ6 br
1
A) 96 B) 90 C) 84 D) 80 E) 76
2 h = 2 br
ñ6 1 2
2
V = π.r . h = π.(ñ6) .2 = 4π br 3
1
Çözüm: 1 3 3
P
Yanal Alan = π.r.a
a a=10 II. bir koni olup
h 60π = πr.10 ⇒ r = 6 cm
POB dik üçgeninde r = ñ6 br
r=6 2
A O B Pisagor Bağıntısı’ndan 3 h = 3 br
2
2
2
2
2
2
h + 6 = 10 ⇒ h = 8 cm’dir. ñ6 V = π.r . h = π.(ñ6) . 3 = 6π br 3
2
2
2
1
2
3
Hacim = π6 .8 = 96π cm bulunur. 3 3
3 V + V = 4π + 6π = 10π br bulunur.
3
1 2
57