Page 64 - Geometri Çalışma Yaprakları - Giriş Yayınları

TYT GEOMETRİ 6. BÖLÜM: DOĞRUNUN ANALİTİĞİ

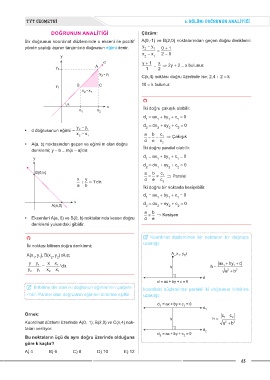
DOĞRUNUN ANALİTİĞİ Çözüm:

Bir doğrunun koordinat düzleminde x ekseni ile pozitif A(0,-1) ve B(2,0) noktalarından geçen doğru denklemi:
yönde yaptığı açının tanjantına doğrunun eğimi denir. y - y = 0 + 1
2
1
x - x 2 - 0
y 2 1
d y + 1 x
y 2 A 1 = ⇒ 2y + 2 = x bulunur.
2
y - y 1 C(k,4) noktası doğru üzerinde ise; 2.4 + 2 = k
2
y 1 B C 10 = k bulunur.
x - x 1
2
Ÿ
α x
x 1 x 2 İki doğru çakışık olabilir.
d = ax + by + c = 0
1 1 1 1
y - y d = dx + ey + c = 0
2
2
2
2
• d doğrusunun eğimi = 2 1
x - x a b c
2 1 = = 1 ⇒ Çakışık
d e c
• A(a, b) noktasından geçen ve eğimi m olan doğru 2
denklemi; y - b = m(x - a)’dır. İki doğru paralel olabilir.
y d = ax + by + c = 0
1
1
1
1
d = dx + ey + c = 0
2 1 2 2
B(0,b) a b c 1
x + y = 1'dir. d = e ≠ c 2 ⇒ Paralel
a b İki doğru bir noktada kesişebilir.
d = ax + by + c = 0
1 1 1 1
x d = dx + ey + c = 0
A(a,0) 2 2 2 2
a ≠ b ⇒ Kesişen
• Eksenleri A(a, 0) ve B(0, b) noktalarında kesen doğru d e
denklemi yukarıdaki gibidir.

Ÿ { Koordinat düzleminde bir noktanın bir doğruya
İki noktası bilinen doğru denklemi; uzaklığı;

A(x , y ), B(x , y ) olup; A_x , y i
1
1
2
1
1
2
y − y 1 = x − x 1 'dir. ax + 1 by + 1 c
y − y x − x h h = 2 2
2 1 2 1 a + b
d
d = ax + by + c = 0
{ Birbirine dik olan iki doğrunun eğimlerinin çarpımı koordinat düzleminde paralel iki doğrunun birbirine
-1’dir. Paralel olan doğruların eğimleri birbirine eşittir. uzaklığı;
d = ax + by + c = 0
1
1
d 1
Örnek: c - c
h h = 1 2
Koordinat düzlemi üzerinde A(0,-1), B(2,0) ve C(k,4) nok- a + b 2
2
taları veriliyor. d
d = ax + by + c = 0 2
Bu noktaların üçü de aynı doğru üzerinde olduğuna 2 2
göre k kaçtır?
A) 4 B) 6 C) 8 D) 10 E) 12

63