Page 73 - 8. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

ÖZDEŞLIKLER
ÖZDEŞLIKLER 3. ÜNİTE 73
• Içerdiği değişken veya değişkenlerin alabileceği her gerçek sayı için doğru olan eşitliklere özdeşlik denir.
• Içerdiği değişken veya değişkenlerin alabileceği bazı değerler için doğru olan eşitliklere denklem denir.
• 3 tane çok önemli özdeşliğimiz vardır.

ÖNEMLI ÖZDEŞLIKLER
1� Iki sayının toplamının karesi 2� Iki sayının farkının karesi 3� Iki kare farkı
2
2
2
2
2
2
(a + b) = a + 2ab + b 2 (a - b) = a - 2ab + b 2 a - b = (a - b) (a + b)
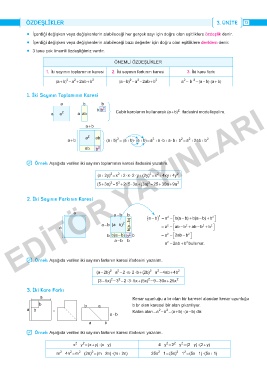
1. İki Sayının Toplamının Karesi
EDİTÖR YAYINLARI
a b b
b b 2 2
a a 2 a ab Cebir karolarını kullanarak (a + b) ifadesini modelleyelim.
a + b

.
.
.
2
2
2
2
a + b a 2 ab (a + b) = (a + b) (a + b) = a + a b + a b + b = a + 2ab + b 2
ab b 2
̛ Örnek: Aşağıda verilen iki sayının toplamının karesi ifadesini yazalım.
. . .
2
2
2
2
(x + 2y) = x + 2 x 2 y + (2y) = x + 4xy + 4y 2
. .
2
2
2
(5 + 3a) = 5 + 2 5 3a + (3a) = 25 + 30a + 9a 2
2. İki Sayının Farkının Karesi
a a - b b ( − ab ) = 2 2 −a  − + − + 2 b(ab) b(ab) b
a - b (a - b) 2 b(a - b) 2  2 2 2 
a = − a   − + −ab b + b ab b 
2
b b(a - b) b b a 2 −  =  − 2 2ab b 
a - b b
2
= 2 − a + 2ab b bulunur.

̛ Örnek: Aşağıda verilen iki sayının farkının karesi ifadesini yazalım.
. . .
2
2
2
2
(a - 2b) = a - 2 a 2 b + (2b) = a - 4ab + 4b 2
. .
2
2
2
(3 - 5x) = 3 - 2 3 5x + (5x) = 9 - 30x + 25x 2
3. İki Kare Farkı
a Kenar uzunluğu a br olan bir karesel alandan kenar uzunluğu
b b a b br olan karesel bir alan çıkarılıyor.
a b = Kalan alan = a - b = (a + b) (a - b) dir.
.
2
2
a - b
a b
̛ Örnek: Aşağıda verilen iki sayının farkının karesi ifadesini yazalım.
.
.
2
2
2
2
2
x - y = (x + y) (x - y) 4 - y = 2 - y = (2 - y) (2 + y)
.
.
2
2
2
2
2
2
2
m - 4n = m - (2n) = (m - 2n) (m + 2n) 25x - 1 = (5x) - 1 = (5x - 1) (5x + 1)