Page 35 - 9-sinif-matematik-odn

ÜÇGENLER 149
Şekilde bir hayvan barınağının görüntüsü bulun-
Örnek:
maktadır. barınağın boyalı olan üçgensel bölge-
A nin ölçüleri 5 m, 5 m ve 8 m’dir. Bu üçgensel bölge
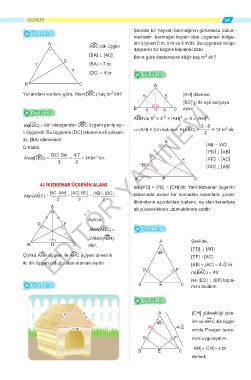
A¿BC dik üçgen
dayanıklı bir kağıtla kaplanacaktır.
[BA] ⊥ [AC] Buna göre kaplanacak kâğıt kaç m dir?
2
D
7 |BA| = 7 br
4
|DC| = 4 br Çözüm:
B C A
2
Yukarıdaki verilere göre, Alan(D¿BC) kaç br ’dir? 5 5 [AH] dikmesi
EDİTÖR YAYINEVİ
[BC]’yi iki eşit parçaya
B 4 H 4 C ayırır.
Çözüm:
2
2
2
2
A¿BH’de 5 = 4 + |AH| ⇒ 9 = |AH|
m(BDC)é > 90 olduğundan D¿BC üçgeni geniş açı- 3 . 8 2
o
lı üçgendir. Bu üçgende [DC] tabanına ait yüksek- ⇒ |AH| = 3 m bulunur. A(A¿BC) = 2 = 12 m dir.
lik, [BA] dikmesidir. A
O halde, AB = AC
[PD ] [ AB ]
⊥
¿
2
Alan(DBC) = DC . BA = 4.7 = 14 br 'dir. H [PE ] [AC ]
⊥
2 2 E
D [CH ] [ AB ]
⊥
B P C
4) İKİZKENAR ÜÇGENİN ALANI
ise |PD| + |PE| = |CH|’dir. Yani ikizkenar üçgenin
∆ BC . AH AC . BE | AB |.|DC | tabanında alınan bir noktadan kenarlara çizilen
Alan(ABC) = = =
2 2 2 dikmelerin uzunlukları toplamı, eş olan kenarlara
A
ait yüksekliklerin uzunluklarına eşittir.
Ayrıca;
D E
Alan(ABC)¿ = Örnek:
2Alan(ABH)¿ Şekilde;
B H C olur. A
[ED] ⊥ [AB]
Çünkü A¿BH üçgeni ile A¿HC üçgeni simetrik 45 o [EF] ⊥[AC]
iki dik üçgen olduğundan alanları eşittir. |AB| = |AC| = 4ñ2 br
D F
m(BéAC) = 45°
ise |ED| + |EF| topla-
Örnek: B E C mını bulalım.

Çözüm:

5 m 5 m A [CH] yüksekliği çize-
45 o lim ve A¿HC dik üçge-
8 m H 4ñ2 ninde Pisagor teore-
D F mini uygulayalım.

AH = CH = x br
B E C
dersek