Page 32 - 9-sinif-matematik-odn

132 ÜÇGENLER
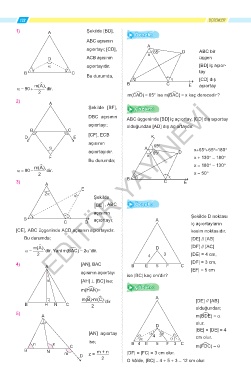
1) A Şekilde [BD], Örnek:

ABC açısının
A
açıortayı; [CD], 65 o D ABC bir
x
D ACB açısının üçgen
α açıortayıdır. [BD] iç açıor-
B C tay
Bu durumda,
[CD] dış

m(A) B C E açıortay
α= 90 + 'dir.
2

o
m(CAD) = 65 ise m(BAC) = x kaç derecedir?
2) A
Şekilde [BF], Çözüm:
DBC açısının ABC üçgeninde [BD] iç açıortay, [CD] dış açıortay
açıortayı; olduğundan [AD] dış açıortaydır.
B C
D E [CF], ECB K
açısının
α A 65 o
açıortayıdır. 65 o D x+65°+65°=180°
F x x + 130° = 180°
Bu durumda;

m(A) x = 180° - 130°
α= 90 − 'dir.
2 İTÖR YAYINEVİ x = 50°
3) A B C E
E
2α α Şekilde
[ ] Örnek:
BE , ABC
açısının
B açıortayı; A Şekilde D noktası
C D iç açıortayların
[CE], ABC üçgeninde ACD açısının açıortayıdır. kesim noktasıdır.
Bu durumda; [DE] // [AB]

m(A) D [DF] // [AC]
2 'dir.
α= 'dir. Yani m(BAC) = α
2 ED 4 3 |DE| = 4 cm,
4) A [AN], BAC B E 5 F C |DF| = 3 cm,
|EF| = 5 cm
açısının açıortayı
α [AH] ⊥ [BC] ise; ise |BC| kaç cm’dir?
Çözüm:
m(HéAN)=
m(ëB)-m(ëC) ’dir. A [DE] // [AB]
B H N C 2 olduğundan;
5)
A m(BéDE) = a
olur.
D
[AN] açıortay α α 4 3 θ θ |BE| = |DE| = 4
cm olur.
n z C ise; B 4 α E 5 F θ 3 C m(FéDC) = θ
B N m z = m + n |DF| = |FC| = 3 cm olur.
D
2 O hâlde, |BC| = 4 + 5 + 3 = 12 cm olur.