Page 38 - Geometri Çalışma Yaprakları - Giriş Yayınları

TYT GEOMETRİ 3. BÖLÜM: PARALELKENAR

PARALELKENAR Paralelkenarda Alan

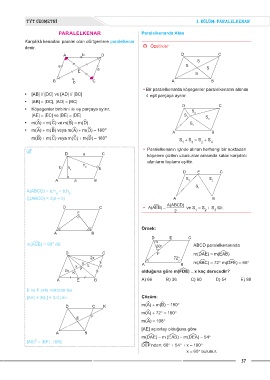
Karşılıklı kenarları paralel olan dörtgenlere paralelkenar
denir. Ÿ Özellikler
A b D D C
S
a S S
E a
S
B b C A B
• Bir paralelkenarda köşegenler paralelkenarın alanını
• [AB] // [DC] ve [AD] // [BC] 4 eşit parçaya ayrılır.
• |AB| = |DC|, |AD| = |BC|
D C
• Köşegenler birbirini iki eş parçaya ayırır. S
|AE| = |EC| ve |BE| = |DE| S 1 4 S
• m(ëA) = m(ëC) ve m(ëB) = m(ëD) S 3
2
o
• m(ëA) + m(ëB) veya m(ëA) + m(ëD) = 180 A B
m(ëB) + m(ëC) veya m(ëC) + m(ëD) = 180 o S + S = S + S
1 3 2 4
{ • Paralelkenarın içinde alınan herhangi bir noktadan
D a C köşelere çizilen uzunluklar arasında kalan karşılıklı
alanların toplamı eşittir.
h
b h b
a b
D E C
A a B S 3 S 2
S 1
A(ABCD) = a.h = b.h
a b
Ç(ABCD) = 2(a + b) A B

D C • A(AEB)ÿ = A(ABCD) ve S = S + S tür.
E 2 1 2 3

Örnek:
A B
D E C
o
m(AéEB) = 90 dir. x 66 o ABCD paralelkenarında
D C F m(DéAE) = m(EéAB)
2x 72 o
x A B m(AéBC) = 72° m(DéFE) = 66°
x L F
2x P
K olduğuna göre m(FéDE) = x kaç derecedir?
A E B A) 66 B) 36 C) 60 D) 54 E) 88

E ve F orta noktalar ise
|AK| = |KL| = |LC| dir. Çözüm:

D C K m(ëA) + m(ëB) = 180°
m(ëA) + 72° = 180°
E F
m(ëA) = 108°
[AE] açıortay olduğuna göre
A B
m(DéAE) = m (EéAB) = m(DéEA) = 54°
2
|AE| = |EF| . |EK|
DÿEF'nden; 66° + 54° + x = 180°
x = 60° bulunur.

37