Page 36 - Geometri Çalışma Yaprakları - Giriş Yayınları

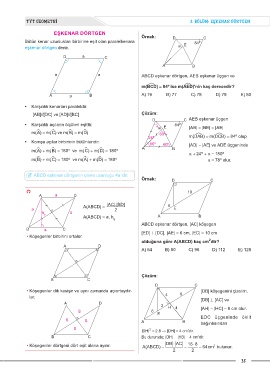
TYT GEOMETRİ 3. BÖLÜM: EŞKENAR DÖRTGEN

EŞKENAR DÖRTGEN
Örnek: D C
Bütün kenar uzunlukları birbirine eşit olan paralelkenara E 84º
eşkenar dörtgen denir. α
D a C

A B
a a ABCD eşkenar dörtgen, AEB eşkenar üçgen ve

m(BéCD) = 84º ise m(AéED)'nin kaç derecedir?
A a B A) 76 B) 77 C) 78 D) 79 E) 80

• Karşılıklı kenarları paraleldir.

[AB]//[DC] ve [AD]//[BC] Çözüm:
D C AEB eşkenar üçgen
• Karşılıklı açıların ölçüleri eşittir. α α E 84º |AB| = |BE| = |AE|

m(ëA) = m(ëC) ve m(ëB) = m(ëD) 60º
24º m(DéAB) = m(DéCB) = 84º olup
• Komşu açılar birbirinin bütünleridir. 60º 60º |AD| = |AE| ve ADE üçgeninde

m(ëA) + m(ëB) = 180º ve m(ëC) + m(ëD) = 180º A B
o
a + 24 + a = 180º
m(ëB) + m(ëC) = 180º ve m(ëA) + m(ëD) = 180º a = 78º olur.

{ ABCD eşkenar dörtgenin çevre uzunluğu 4a 'dır.
Örnek: D C

Ÿ 10
A a D

A(ABCD) = |AC|.|BD| 6
a 2 E
h a a
A(ABCD) = a. h a A B
ABCD eşkenar dörtgen, [AC] köşegen
B a C
• Köşegenler birbirini ortalar. [ED] ⊥ [DC], |AE| = 6 cm, |EC| = 10 cm
2
olduğuna göre A(ABCD) kaç cm dir?
A D
A) 64 B) 80 C) 96 D) 112 E) 128

Çözüm:
B C
D C
• Köşegenler dik kesişir ve aynı zamanda açıortaydır- 8 [DB] köşegenini çizelim.
lar. 4 [DB] ⊥ [AC] ve
A D
2 H 4 |AH| = |HC| = 8 cm olur.
S 6 E

S S A B EDC üçgeninde öklit
bağıntısından
S |DH| = 2.8 ⇒ |DH| = 4 cm’dir.
2
B C Bu durumda; |DH| = |HB| = 4 cm'dir.

• Köşegenler dörtgeni dört eşit alana ayırır. A(ABCD) = DB AC⋅ = 16 8 ⋅ = 64cm bulunur.
2
2 2
35