Page 12 - 11. SINIF MATEMATİK KAZANIM ODAKLI ve BECERİ TEMELLİ SORU BANKASI

ÖZETİN ÖZETİ ÜNİTE 1: TRİGONOMETRİ

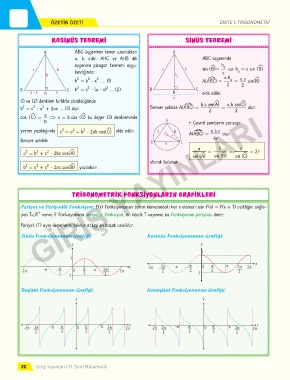
KOSİNÜS TEOREMİ SİNÜS TEOREMİ

A ABC üçgeninin kenar uzunlukları A
a, b, c'dir. AHC ve AHB dik ABC üçgeninde
üçgenine pisagor teoremi uygu- h a
c b landığında; c b sin (ëB)= ⇒ h = c sin (ëB)
a
h h a c a.h
2
2
2
h = b - x .... (1) A(A¿BC) = a = a.c sin(ëB)
2 2
2
2
2
B C h = c - (a - x) ... (2) B C
a - x H x H elde edilir.
a
(1) ve (2) denklem birlikte çözüldüğünde b.c sin(ëA) a.b sin(ëC)
2
2
2
b = c - a + 2ax ... (3) olur. Benzer şekilde A(A¿BC) = 2 = 2 olur.
GİRİŞ YAYINLARI
x
cos (ëC ) = ⇒ x = b.cos (ëC) bu değer (3) denkleminde
b A r: Çevrel çemberin yarıçapı
2
yerine yazıldığında c = a + b - 2ab cos(ëC) elde edilir. c O r b A(A¿BC) = a.b.c olur.
2
2
Benzer şekilde B a C 4r
a b c
2
2
2
a = b + c - 2bc cos(ëA) = = = 2r
sin (ëA) sin (ëB) sin (ëC)
olarak bulunur.
2
2
2
b = a + c - 2ac cos(ëB) yazılabilir.
trİgonometrİk fonksİyonların grafİklerİ
Periyot ve Periyodik Fonksiyon: f(x) fonksiyonunun tanım kümesindeki her x elemanı için f(x) = f(x + T) eşitliğini sağla-
+
yan T∈R varsa f fonksiyonuna periyodik fonksiyon, en küçük T sayısına bu fonksiyonun periyodu denir.
Periyot (T) aynı değerlerin tekrar ettiği en küçük aralıktır.
Sinüs Fonksiyonunun Grafiği: Kosinüs Fonksiyonunun Grafiği:
y y
1
1 x

-2π -π - π 0 π π 3π 2π x -2π - 3π -π - π 2 0 π 2 π 3π 2π
2
2
2 2 2 -1
-1
Tanjant Fonksiyonunun Grafiği: Kotanjant Fonksiyonunun Grafiği:
y y

-2π 3π -π - π 0 π π 3π 2π x -2π 3π -π - π 0 π π 3π 2π x
2 2 2 2 2 2 2 2

22 Giriş Yayınları / 11. Sınıf Matematik