Page 18 - 9-sinif-matematik-odn

52 DENKLEM VE EŞİTSİZLİKLER

Örnek: Örnek:

x, y ∈ R olmak üzere,
1 < x < 4
-5 < y < -1 ise x+y ‘nin en büyük tam sayı değeri
nedir?

Çözüm:

x, y ∈ R olduğu için eşitsizlik düzenlenir. O halde;
6x + 12 > 5x + 45EDİTÖR YAYINEVİ
x+y toplamını elde etmek için eşitsizlikleri topla-
x 3 3 3 yalım. Bu durumda;
x 3 3 3
x 3 3 3 1x< < 4
x 3 3 3 x x x x x x + − 5 < y <− 1
x 3 3 3 1 1 1 x y
−
1 1 1 15− <+< 4 1 olur.
xy
1 1 1 − 4 <+< 3
1 1 1
x+y’nin en büyük tam sayı değeri 2’dir.
Şimdi aynı örneği tam sayılar için inceleyelim. x,
y ∈ Z olmak üzere x+y toplamının en büyük değe-
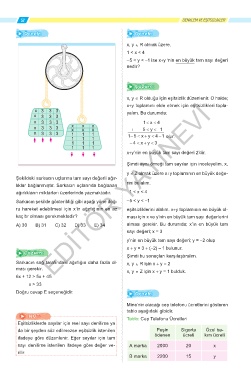
Şekildeki sarkacın uçlarına tam sayı değerli ağır-
lıklar bağlanmıştır. Sarkacın uçlarında bağlanan rini bulalım.
ağırlıkların miktarları üzerlerinde yazmaktadır. 1 < x < 4
Sarkacın şekilde gösterildiği gibi aşağı yöne doğ- -5 < y < -1
ru hareket edebilmesi için x’in ağırlığının en az eşitsizliklerini alalım. x+y toplamının en büyük ol-
kaç br olması gerekmektedir? ması için x ve y’nin en büyük tam sayı değerlerini
A) 30 B) 31 C) 32 D) 33 E) 34 alması gerekir. Bu durumda; x’in en büyük tam
sayı değeri; x = 3

y’nin en büyük tam sayı değeri; y = -2 olup
x + y = 3 + (-2) = 1 bulunur.
Çözüm:
Şimdi bu sonuçları karşılaştıralım.
Sarkacın sağ tarafındaki ağırlığın daha fazla ol- x, y ∈ R için x + y = 2
ması gerekir.
x, y ∈ Z için x + y = 1 bulduk.

x > 33
Doğru cevap E seçeneğidir. Örnek:

Mine’nin alacağı cep telefonu ücretlerini gösteren
tablo aşağıdaki gibidir.
NOT: Tablo: Cep Telefonu Ücretleri
Eşitsizliklerde sayılar için reel sayı denilirse ya
da bir şeyden söz edilmezse eşitsizlik istenilen Peşin Sigorta Özel ba-
ifadeye göre düzenlenir. Eğer sayılar için tam ödenen ücreti kım ücreti
sayı denilirse istenilen ifadeye göre değer ve- A marka 2000 20 x
rilir.
B marka 2200 15 y