Page 8 - Geometri Çalışma Yaprakları - Giriş Yayınları
P. 8
TYT GEOMETRİ 2. BÖLÜM: DİK ÜÇGEN (PİSAGOR - ÖKLİD)
DİK ÜÇGEN (PİSAGOR - ÖKLİD) Kenarlarına Göre Özel Dik Üçgenler
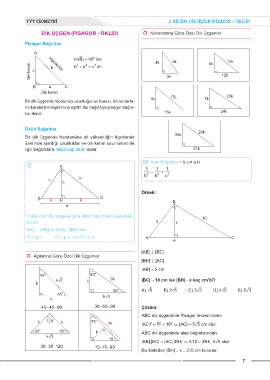
Pisagor Bağıntısı
A
o
m(ëB) = 90 ise 4k 5k 5k 13k
2
Dik kenar c b b = a + c dir. 3k 12k
2
2
Hipotenüs
B a C
Dik kenar
8k 17k 7k 25k
Bir dik üçgende hipotenüs uzunluğunun karesi, dik kenarla-
rın karelerinin toplamına eşittir. Bu bağıntıya pisagor bağın-
tısı denir. 15k 24k
Öklid Bağıntısı
20k 29k
Bir dik üçgende hipotenüse ait yüksekliğin hipotenüs
üzerinde ayırdığı uzunluklar ve dik kenar uzunlukları ile
ilgili bağıntılara öklid bağıntıları denir. 21k
{ Alan Bağıntısı = b.c = a.h
{ A
1 = 1 + 1
h 2 b 2 c 2
c b
h
Örnek:
B p H k C B
a
Yukarıdaki dik üçgene göre öklid bağıntıları aşağıdaki 10
gibidir. 5 x
[AC] ⊥ [AB] ve [AH] ⊥ [BC] ise
2
2
2
h = p.k c = p.a ve b = k.a A C
H
[AB] ⊥ [BC]
Açılarına Göre Özel Dik Üçgenler
[BH] ⊥ [AC]
|AB| = 5 cm
45° 60°
kñ2 k 2k |BC| = 10 cm ise |BH| = x kaç cm'di?
k
30° A) ñ5 B) 2ñ5 C) 3ñ3 D) 4ñ5 E) 5ñ3
45° kñ3
k
45-45-90 30-60-90 Çözüm:
ABC dik üçgeninde Pisagor teoreminden
k 120° k 75° 4k |AC| = 5 + 10 ⇒ |AC| = 5ñ5 cm olur.
2
2
2
30° 30° k ABC dik üçgeninde alan bağıntısından
kñ3
15°
|AB|.|BC| = |AC|.|BH| ⇒ 5.10 = |BH|. 5ñ5 olur.
30-30-120 15-75-90
Bu ifadeden |BH| = x = 2ñ5 cm bulunur.
7