Page 12 - Geometri Çalışma Yaprakları - Giriş Yayınları

TYT GEOMETRİ 2. BÖLÜM: EŞKENAR ÜÇGEN

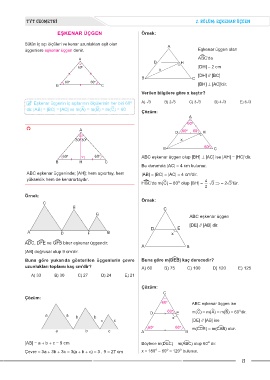
EŞKENAR ÜÇGEN Örnek:

Bütün iç açı ölçüleri ve kenar uzunlukları eşit olan A
üçgenlere eşkenar üçgen denir. Eşkenar üçgen olan

A A¿BC'de
D H
60 o x |DH| = 2 cm
[DH] // [BC]
B C
60 o 60 o
B C [BH] ⊥ [AC]'dir.
Verilen bilgilere göre x kaçtır?

o
{ Eşkenar üçgenin iç açılarının ölçülerinin her biri 60 A) ñ3 B) 2ñ3 C) 3ñ3 D) 4ñ3 E) 6ñ3
dir. |AB| = |BC| = |AC| ve m(ëA) = m(ëB) = m(ëC) = 60 Çözüm:
A
60 o
Ÿ A o o
D 60 60 H
30 o 30 o x
B 60 o C
60 o 60 o ABC eşkenar üçgen olup [BH] ⊥ [AC] ise |AH| = |HC|'dir.
B H C
Bu durumda |AC| = 4 cm bulunur.
ABC eşkenar üçgeninde; [AH]; hem açıortay, hem |AB| = |BC| = |AC| = 4 cm'dir.
yükseklik hem de kenarortaydır. 4
o
H¿BC'de m(ëC) = 60 olup |BH| = ñ3 ⇒ = 2ñ3'tür.
2
Örnek:
Örnek:
C
E C
G
ABC eşkenar üçgen
[DE] // [AB] dir.
D E
A D F B x

A¿DC, D¿FE ve G¿FB birer eşkenar üçgendir.
A B
[AB] doğrusal olup 9 cm’dir.

Buna göre yukarıda gösterilen üçgenlerin çevre Buna göre m(DéEB) kaç derecedir?
uzunlukları toplamı kaç cm’dir? A) 60 B) 75 C) 100 D) 120 E) 125

A) 33 B) 30 C) 27 D) 24 E) 21

Çözüm:
C
Çözüm:
60 o ABC eşkenar üçgen ise
o
D 60 o E m(ëC) = m(ëA) = m(ëB) = 60 dir.
a a b b x
c c [DE] // [AB] ise
60 o 60 o m(CéDE) = m(CéAB) olur.
a b c A B

o
[AB] = a + b + c = 9 cm Böylece m(DéEC) = m(AéBC) olup 60 dir.
o
o
o
Çevre = 3a + 3b + 3c = 3(a + b + c) = 3 . 9 = 27 cm x = 180 - 60 = 120 bulunur.
11