Page 16 - Geometri Çalışma Yaprakları - Giriş Yayınları

TYT GEOMETRİ 2. BÖLÜM: KENARORTAY

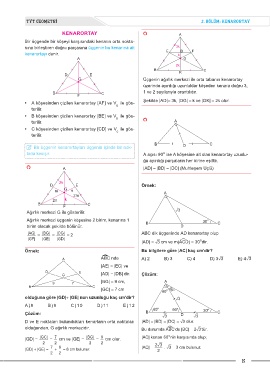
KENARORTAY Ÿ A

Bir üçgende bir köşeyi karşısındaki kenarın orta nokta-
sına birleştiren doğru parçasına üçgenin bu kenarına ait 3k
kenarortayı denir. E k D F
A G
2k
B C
D E K
G Üçgenin ağırlık merkezi ile orta tabanın kenarortay
üzerinde ayırdığı uzunluklar köşeden kenara doğru 3,

B C 1 ve 2 sayılarıyla orantılıdır.
F
Şekilde |AD|= 3k, |DG| = k ve |GK| = 2k olur.
• A köşesinden çizilen kenarortay [AF] ve V ile gös-
a
terilir.
• B köşesinden çizilen kenarortay [BE] ve V ile gös-
b
terilir. Ÿ A
• C köşesinden çizilen kenarortay [CD] ve V ile gös-
c
terilir.
B D C
{ Bir üçgenin kenarortayları üçgenin içinde bir nok-
tada kesişir. A açısı 90 ise A köşesine ait olan kenarortay uzunlu-
o
ğu ayırdığı parçaların her birine eşittir.

Ÿ A |AD| = |BD| = |DC| (Muhteşem Üçlü)

2k
D E Örnek:
m G n A
2m
2n k
B C
F
Ağırlık merkezi G ile gösterilir. ñ3
Ağırlık merkezi üçgenin köşesine 2 birim, kenarına 1 B 30 o C
birim olacak şekilde bölünür. D
|AG| = |BG| = |CG| = 2 ABC dik üçgeninde AD kenarortay olup
|GF| |GE| |GD|
o
|AD| = ñ3 cm ve m(AéCD) = 30 dir.
Örnek: Bu bilgilere göre |AC| kaç cm’dir?
A A¿BC nde A) 2 B) 3 C) 4 D) 3ñ3 E) 4ñ3
|AE| = |EC| ve
D E
G |AD| = |DB| dir. Çözüm:
9 7 |BG| = 9 cm, A
B C
|GC| = 7 cm 60 o 30 o
olduğuna göre |GD|+ |GE| nun uzunluğu kaç cm'dir? ñ3
A ) 8 B ) 9 C) 10 D) 11 E ) 12 60 o 60 o o

Çözüm: B D 30 C
ñ3 ñ3
D ve E noktaları bulundukları kenarların orta noktaları |AD| = |BD| = |DC| = ñ3 olur.
olduğundan, G ağırlık merkezidir. Bu durumda A¿BC’de |BC| = 2ñ3’tür.
o
9
7
|GD| = |GC| = cm ve |GE| = |BG| = cm olur. |AC| kenarı 60 nin karşısında olup;
2 2 2 2 2ñ3
|GD| + |GE| = 7 + 9 = 8 cm bulunur. |AC| = 2 . ñ3 = 3 cm bulunur.
2 2
15