Page 23 - 6. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

KALANSIZ BÖLÜNEBİLME KURALLARI (5, 6, ⒐, 10 İLEİLE))
KALANSIZ BÖLÜNEBİLME KURALLARI (5, 6, ⒐, 10 1. ÜNİTE 23
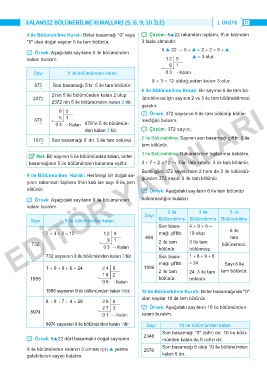
5 ile Bölünebilme Kuralı: Birler basamağı "0" veya ̚ Çözüm: 5▲22 rakamları toplamı, 9'un katından
"5" olan doğal sayılar 5 ile tam bölünür. 3 fazla olmalıdır.

̛ Örnek: Aşağıdaki sayıların 5 ile bölümünden 5 ▲ 22 → 5 + ▲ + 2 + 2 = 9 + ▲
kalanı bulalım. 1 2 9 ▲ = 3 olur.
9 1
Sayı 5 ile bölümünden kalan 0 3 → Kalan
9 + 3 = 12 olduğundan kalan 3 olur.
975 Son basamağı 5'tir. 5 ile tam bölünür.
6 ile Bölünebilme Kuralı: Bir sayının 6 ile tam bö-
2’nin 5 ile bölümünden kalan 2 olup
2372 lünebilmesi için sayının 2 ve 3 ile tam bölünebilmesi
2372 nin 5 ile bölümünden kalan 2 dir.
EDİTÖR YAYINLARI
gerekir.
8 5 ̛ Örnek: 372 sayısının 6 ile tam bölünüp bölün-
678 5 1 mediğini bulalım.
0 3 → Kalan 678'in 5 ile bölümün-
den kalan 3 tür. ̚ Çözüm: 372 sayısı;

1570 Son basamağı 0' dır. 5 ile tam bölünür. 2 ile Bölünebilme; Sayının son basamağı çifttir. 2 ile
tam bölünür.
3 ile Bölünebilme; Rakamlarının toplamına bakalım.
{ Not: Bir sayının 5 ile bölümünden kalan, birler
basamağının 5 ile bölümünden kalanına eşittir. 3 + 7 + 2 = 12 → 3’ün tam katıdır. 3 ile tam bölünür.
Buna göre 372 sayısı hem 2 hem de 3 ile bölündü-
9 ile Bölünebilme Kuralı: Herhangi bir doğal sa- ğünden 372 sayısı 6 ile tam bölünür.
yının rakamları toplamı 9'un katı ise sayı 9 ile tam
bölünür. ̛ Örnek: Aşağıdaki sayıların 6 ile tam bölünüp

̛ Örnek: Aşağıdaki sayıların 9 ile bölümünden bölünmediğini bulalım.
kalanı bulalım.
2 ile 3 ile 6 ile
Sayı
Sayı 9 ile bölümünden kalan Bölünebilme Bölünebilme Bölünebilme
Son basa- 4 + 9 + 6 =
7 + 3 + 2 = 12 1 2 9 mağı çifttir. 19 olup 6 ile
9 1 496 2 ile tam 3 ile tam tam
732 bölünemez.
0 3 → Kalan bölünür. bölünmez.
732 sayısının 9 ile bölümünden kalan 3’tür. Son basa- 1 + 8 + 9 + 6
mağı çifttir. = 24 Sayı 6 ile
1 + 9 + 8 + 6 = 24 2 4 9 1896 2 ile tam tam bölünür.
1 8 2 24; 3 ile tam
1986 bölünür. bölünür.
0 6 → Kalan
1986 sayısının 9 ile bölümünden kalan 6’dır. 10 ile Bölünebilme Kuralı: Birler basamağında "0"
olan sayılar 10 ile tam bölünür.
8 + 9 + 7 + 4 = 28 2 8 9
2 7 3 ̛ Örnek: Aşağıdaki sayıların 10 ile bölümünden
8974
0 1 → Kalan kalanı bulalım.
8974 sayısının 9 ile bölümünden kalan 1’dir. Sayı 10 ile bölümünden kalan
Son basamağı "0" (sıfır) dır. 10 ile bölü-
̛ Örnek: 5▲22 dört basamaklı doğal sayısının 2340 münden kalan da 0 (sıfır) dır.

9 ile bölümünden kalanın 3 olması için ▲ yerine 2576 Son basamağı 6 olup 10 ile bölümünden
gelebilecek sayıyı bulalım. kalan 6 dır.