Page 22 - 11. SINIF MATEMATİK KAZANIM ODAKLI ve BECERİ TEMELLİ SORU BANKASI

ÖZETİN ÖZETİ ÜNİTE 3: FONKSİYONLARDA UYGULAMALAR

fonksİyonlarLa İLGİLİ uygulamalar

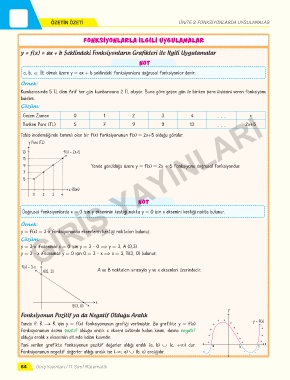
y = f(x) = ax + b Şeklindeki Fonksiyonların Grafikleri ile İlgili Uygulamalar

NOT
a, b, ∈  olmak üzere y = ax + b şeklindeki fonksiyonlara doğrusal fonksiyonlar denir.

Örnek:
Kumbarasında 5 TL olan Arif her gün kumbarasına 2 TL atıyor. Buna göre geçen gün ile biriken para ilişkisini veren fonksiyonu
bulalım.
Çözüm:
f(x) = 3-xGİRİŞ YAYINLARI
Geçen Zaman 0 1 2 3 4 . . . x

Biriken Para (TL) 5 7 9 11 13 . . . 2x+5
Tablo incelendiğinde tanımlı olan bir f(x) fonksiyonunun f(x) = 2x+5 olduğu görülür.
y Para (TL)

13 f(x) = 2x+5
11
9 Yanda görüldüğü üzere y = f(x) = 2x + 5 fonksiyonu doğrusal fonksiyondur.
7
5

x (Gün)
1 2 3 4
NOT
Doğrusal fonksiyonlarda x = 0 için y ekseninin kestiği nokta y = 0 için x eksenini kestiği nokta bulunur.

Örnek:
y = f(x) = 3-x fonksiyonunda eksenlerin kestiği noktaları bulunuz.
Çözüm:
y = 3-x ifadesinde x = 0 için y = 3 - 0 ⇒ y = 3, A (0,3)
y = 3 - x ifadesinde y = 0 için 0 = 3 - x ⇒ x = 3, B(3, 0) bulunur.

y
A(0, 3) A ve B noktaları sırasıyla y ve x eksenleri üzerindedir.

x
B(3, 0)
y
Fonksiyonun Pozitif ya da Negatif Olduğu Aralık
+ + y = f(x)
Yanda f: R → R için y = f(x) fonksiyonunun grafiği verilmiştir. Bu grafikte y = f(x) + +
fonksiyonunun daima pozitif olduğu aralık x ekseni üstünde kalan kısım, daima negatif + + + +
olduğu aralık x ekseninin altında kalan kısımdır. + + +
+ + +
Yani verilen grafikte fonksiyonun pozitif değerler aldığı aralık (a, b) ∪ (c, +∞) dur. a b c x
Fonksiyonunun negatif değerler aldığı aralık ise (-∞, a) ∪ (b, c) aralığıdır. - - - -
- -

64 Giriş Yayınları / 11. Sınıf Matematik