Page 35 - tyt-agresif-matematik

II. Dereceden Denklemler | Fonksyonlar | Polnomlar | Parabol | Karmaşık Sayılar 171

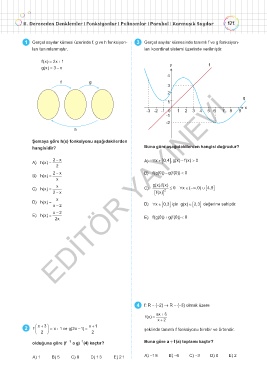
1 Gerçel sayılar kümes� üzer�nde f, g ve h fonks�yon- 3 Gerçel sayılar kümes�nde tanımlı f ve g fonks�yon-
ları tanımlanmıştır. ları koord�nat s�stem� üzer�nde ver�lm�şt�r.

f(x) = 2x 1+
g(x) = 3 x− y f
4
f g
3
2
g
1
x
-3 -2 -1 0 1 2 3 4 5 6 7 8 9
-1
-2
h

Şemaya göre h(x) fonks�yonu aşağıdak�lerden
hang�s�d�r? Buna göre aşağıdak�lerden hang�s� doğrudur?

2x− A) ∀ ∈ [0,4 ],g(x) f(x)− > 0
x
A) h(x) =
2
2x B) f(g(0)) g(f(0))− < 0
−
B) h(x) =
x
x g(x).f(x)
]
≤ 0
∀ ∈ −∞x
(
,0)
∪
C)

C) h(x) = EDİTÖR YAYINEVİ [4,9
2x [f(x) ] 2
−
x
D) h(x) = D) ∀ ∈x ] ]
x2 [0,3 için g(x) ∈ [2,3 değer�ne sah�pt�r.
−
−
x2
E) h(x) =
2x E) f(g(0)) g(f(0))+ < 0

4 f: R − {−2} → R − {−3} olmak üzere

ax 6
+
f(x) =
x2
+
 + x1
+  x 3
2 f   = + x 1 ve g(2x 1) = şekl�nde tanımlı f fonks�yonu b�reb�r ve örtend�r.
−
  2 2
−1
olduğuna göre (f −1 o g) (4) kaçtır? Buna göre a+f (a) toplamı kaçtır?
A) 1 B) 5 C) 9 D) 1 3 E) 21 A) −1 8 B) −6 C) −3 D) 0 E) 2