Page 69 - 6. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

BÖLME İŞLEMİ İLE KESİR İLİŞKİSİ
BÖLME İŞLEMİ İLE KESİR İLİŞKİSİ 3. ÜNİTE 69

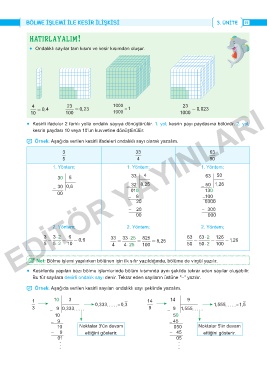
HATIRLAYALIM
• Ondalıklı sayılar tam kısım ve kesir kısımdan oluşur.

2 ⋅TÖR YAYINLARI
4 = 0,4 23 = 0,23 1000 = 1 23 = 0,023
10 100 1000 1000
• Kesirli ifadeler 2 farklı yolla ondalık sayıya dönüştürülür. 1. yol; kesrin payı paydasına bölünür. 2. yol;
kesrin paydası 10 veya 10'un kuvvetine dönüştürülür.

̛ Örnek: Aşağıda verilen kesirli ifadeleri ondalıklı sayı olarak yazalım.

3 33 63
5 4 50
1. Yöntem; 1. Yöntem; 1. Yöntem;

30 5 33 4 63 50
50 1,26
32 8,25
- 30 0,6 - 010 - 130
00
- 8 - 100
20 0300
- 20 - 300
00 2. Yöntem;
000
• EDİ 3 = 3 2 ⋅ = 10 = 0,6 33 = 33⋅ 25 = 825 = 8,25 63 = 63 2 ⋅ 2 ⋅ = 126 = 1,26
2. Yöntem;
2. Yöntem;
6
25
50
5
5
100
50
4⋅
100
4
{
Not: Bölme işlemi yapılırken bölünen için ilk sıfır yazıldığında, bölüme de virgül yazılır.
Kesirlerde yapılan bazı bölme işlemlerinde bölüm kısmında aynı şekilde tekrar eden sayılar oluşabilir.
Bu tür sayılara devirli ondalık sayı denir. Tekrar eden sayıların üstüne "-" yazılır.
̛ Örnek: Aşağıda verilen kesirli sayıları ondalıklı sayı şeklinde yazalım.

1 10 3 14 14 9
3 9 0,333 0,333 = 0,3 9 9 1,555 1,555 = 1,5
- -
10 50
- 9 - 45
10 Noktalar 3'ün devam 050 Noktalar 5'in devam
- 9 ettiğini gösterir. - 45 ettiğini gösterir.
01 05