Page 111 - 11. SINIF MATEMATİK FAVORİ KAZANIM ODAKLI VE BECERİ TEMELLİ SORU BANKASI

ÜNİTE 5: ÇEMBER VE DAİRE ÖZETİN ÖZETİ

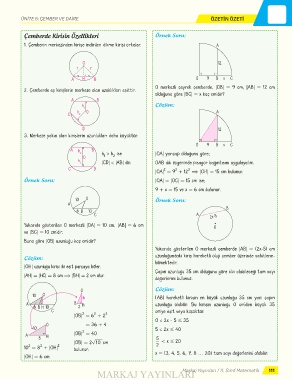
Çemberde Kirişin Özellikleri Örnek Soru:

1. Çemberin merkezinden kirişe indirilen dikme kirişi ortalar. A

O 12
r r

A H B O 9 B x C
O merkezli çeyrek çemberde, |OB| = 9 cm, |AB| = 12 cm
2. Çemberde eş kirişlerin merkeze olan uzaklıkları eşittir.
olduğuna göre |BC| = x kaç cm'dir?
A B
h Çözüm:
1
h O A
C 2

D 12
3. Merkeze yakın olan kirişlerin uzunlukları daha büyüktür.
O 9 B x C
A h B
2 O h > h ise |OA| yarıçap olduğuna göre;
2
1
h 1 |CD| < |AB| dir. OAB dik üçgeninde pisagor bağıntısını uygulayalım.
C D 2 2 2
|OA| = 9 + 12  |OH| = 15 cm bulunur.
Örnek Soru: |OA| = |OC| = 15 cm ise;

9 + x = 15 ve x = 6 cm bulunur.
10 O Örnek Soru:
A
6 B 10 B
C A 2x-5

Yukarıda gösterilen O merkezli |OA| = 10 cm, |AB| = 6 cm O
ve |BC| = 10 cm'dir.

Buna göre |OB| uzunluğu kaç cm'dir?
Yukarıda gösterilen O merkezli çemberde |AB| = (2x-5) cm
uzunluğundaki kiriş hareketli olup çember üzerinde sabitlene-
Çözüm:
bilmektedir.
|OH| uzunluğu kirişi iki eşit parçaya böler.
Çapın uzunluğu 35 cm olduğuna göre x'in alabileceği tam sayı
|AH| = |HC| = 8 cm ⇒ |BH| = 2 cm olur.
değerlerini bulunuz.

O Çözüm:
10 O 6 [AB] hareketli kirişin en büyük uzunluğu 35 cm yani çapın

A B H uzunluğu olabilir. Bu kirişin uzunluğu 0 cm'den büyük 35
6 B H 10 2
C cm'ye eşit veya küçüktür.
2
2
|OB| = 6 + 2 2
0 < 2x - 5 ≤ 35
O = 36 + 4
10 5 < 2x ≤ 40
2
A H |OB| = 40
8 5
|OB| = 2ò10 cm 2 < x ≤ 20
2
2
10 = 8 + |OH| 2 bulunur.
|OH| = 6 cm x = {3, 4, 5, 6, 7, 8 ... 20} tam sayı değerlerini alabilir.
MARKAJ YAYINLARI 111
Markaj Yayınları / 11. Sınıf Matematik