Page 124 - 6. Sınıf Matematik Defterim

5. ÜNİTE ÖZETİN ÖZETİ

ALAN ÖLÇME

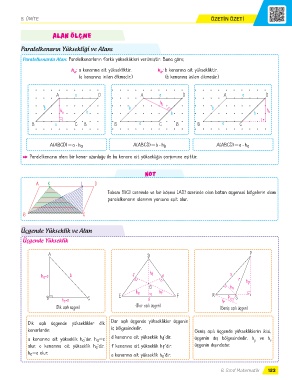
Paralelkenarın Yüksekliği ve Alanı
Paralelkenarda Alan: Paralelkenarların farklı yükseklikleri verilmiştir. Buna göre;

h : a kenarına ait yüksekliktir. h : b kenarına ait yüksekliktir.
a
b
(a kenarına inilen dikmedir.) (b kenarına inilen dikmedir.)

A a D A a D A a D
h b
b b b
h a b b b h a

B a C B B a C B B a C

.
.
.
A(ABCD) = a h a A(ABCD) = b h b A(ABCD) = a h a
Q Paralelkenarın alanı bir kenar uzunluğu ile bu kenara ait yüksekliğin çarpımına eşittir.

NOT

A K L D
Tabanı [BC] üzerinde ve bir köşesi [AD] üzerinde olan bütün üçgensel bölgelerin alanı
paralelkenarın alanının yarısına eşit olur.

B C

Üçgende Yükseklik ve Alan
Üçgende Yükseklik

A D P

h a =c b f hd e s
r hp
G hs
he hf
B h c =a C E d F R hr p S

(Dik açılı üçgen) (Dar açılı üçgen) (Geniş açılı üçgen)

Dik açılı üçgende yükseklikler dik Dar açılı üçgende yükseklikler üçgenin
kenarlardır. iç bölgesindedir. Geniş açılı üçgende yüksekliklerin ikisi,
d
a kenarına ait yükseklik h ’dır. h =c d kenarına ait yükseklik h ’dir. üçgenin dış bölgesindedir. h ve h
a
a
p
r
olur. c kenarına ait yükseklik h ’dir. f kenarına ait yükseklik h ’dir. üçgenin dışındadır.
f
c
h =a olur. e kenarına ait yükseklik h ’dir.
c
e
6. Sınıf Matematik 123