Page 45 - 11. SINIF MATEMATİK KAZANIM ODAKLI ve BECERİ TEMELLİ SORU BANKASI

ÖZETİN ÖZETİ ÜNİTE 5: ÇEMBER VE DAİRE

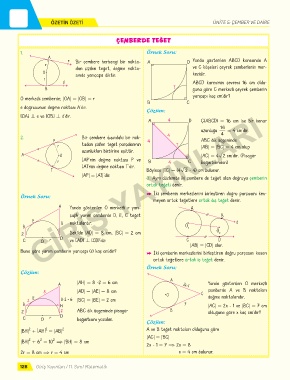
ÇEMBERDE TEĞET

1. Örnek Soru:
A
e Bir çembere herhangi bir nokta- A D Yanda gösterilen ABCD karesinde A
r
dan çizilen teğet, değme nokta- ve C köşeleri çeyrek çemberlerin mer-
O sında yarıçapa diktir. kezidir.
r
d ABCD karesinin çevresi 16 cm oldu-
B T ğuna göre C merkezli çeyrek çemberin
yarıçapı kaç cm'dir?
O merkezli çemberde; |OA| = |OB| = r
B C
e doğrusunun değme noktası A'dır.
GİRİŞ YAYINLARI
Çözüm:
[OA] ⊥ e ve [OB] ⊥ d'dir.
A 4 D Ç(ABCD) = 16 cm ise bir kenar
16
uzunluğu 4 = 4 cm'dir.
2. Bir çembere dışındaki bir nok- 4
P 4 ABC dik üçgeninde
r tadan çizilen teğet parçalarının T |AB| = |BC| = 4 cm olup
uzunlukları birbirine eşittir.
A O |AC| = 4ñ2 cm'dir. (Pisagor
r [AP'nin değme noktası P ve B 4 C bağıntısından)
[AT'nin değme noktası T'dir.
T Böylece |TC| = (4ñ 2 - 4) cm bulunur.
|AP| = |AT|'dir.
3. Aynı düzlemde iki çembere de teğet olan doğruya çemberin
ortak teğeti denir.

Q İki çemberin merkezlerini birleştiren doğru parçasını kes-
Örnek Soru:
meyen ortak teğetlere ortak dış teğet denir.
A Yanda gösterilen O merkezli r yarı- A
çaplı yarım çemberde D, E, C teğet B
E 8 noktalardır. d
B O 1
2 Şekilde |AD| = 8 cm, |BC| = 2 cm O 2
C O r D ve [AD] ⊥ [CD]'dir. C D
|AB| = |CD| olur.
Buna göre yarım çemberin yarıçapı (r) kaç cm'dir? Q İki çemberin merkezlerini birleştiren doğru parçasını kesen
ortak teğetlere ortak iç teğet denir.
Örnek Soru:
Çözüm:
A
A |AH| = 8 -2 = 6 cm 2x-1 Yanda gösterilen O merkezli
8 |AD| = |AE| = 8 cm C çemberde A ve B noktaları
E O değme noktalarıdır.
2 8-2 = 6 |BC| = |BE| = 2 cm
B H 7 |AC| = 2x - 1 ve |BC| = 7 cm
2 2 ABC dik üçgeninde pisagor B olduğuna göre x kaç cm'dir?
C O r D bağıntısını yazalım.
Çözüm:
|
|
2
2
2
|BH| + AH = |AB| A ve B teğet noktaları olduğuna göre
|AC| = |BC|
2
2
2
|BH| + 6 = 10 ⇒ |BH| = 8 cm
2x - 1 = 7 ⇒ 2x = 8
2r = 8 cm ⇒ r = 4 cm x = 4 cm bulunur.
128 Giriş Yayınları / 11. Sınıf Matematik