Page 35 - 11. SINIF MATEMATİK KAZANIM ODAKLI ve BECERİ TEMELLİ SORU BANKASI

ÖZETİN ÖZETİ ÜNİTE 4: DENKLEM VE EŞİTSİZLİK SİSTEMLERİ

İkİncİ dereceden BİR bİlİnmeyenlİ Eşİtsİzlİkler

İkinci Dereceden Bir Bilinmeyenli Eşitsizlikle- Örnek Soru:
2
rin Çözüm Kümesi: a ≠ 0 ve a, b, c ∈ R olmak üzere f(x) = x - 3x + 2 fonksiyonunun işaretini inceleyiniz.
2
2
2
ax + bx + c  0, ax + bx + c ≤ 0, ax + bx + c < 0,
2
ax + bx + c > 0 ifadelerinin her birine ikinci dereceden bir Çözüm:
bilinmeyenli eşitsizlik ve eşitsizliği sağlayan x değerleri küme- x - 3x + 2 = 0 denkleminin katsayıları a = 1, b = -3 ve
2
2
sine eşitsizliğin çözüm kümesi denir. ax + bx + c ikinci dere- c = 2'dir.
ceden üç terimlisinin hangi aralıkta pozitif, hangi aralıkta
2
2
negatif değer olacağı, ax + bx + c = 0 denkleminde ∆ > 0, ∆ = b - 4ac
2
∆ = 0, ∆ < 0 olmak üzere üç durumda incelenir. = (-3) - 4 . 1 . 2
GİRİŞ YAYINLARI
2
2
∆ = b - 4ac > 0 olmak üzere ax + bx + c = 0 denklemi- = 9 - 8 = 1 ve ∆ = 1 > 0'dır.
nin birbirinden farklı iki kökü vardır. Bu kökler x < x olmak Yani f(x) fonksiyonunun iki kökü vardır.
1
2
2
üzere x ve x olsun. Bu durumda ax + bx + c ifadesinin
1 2 x - 3x + 2 = 0 ⇒ (x-2)(x-1) = 0 ise
2
işaret tablosu aşağıdaki gibi incelenir.
x = 2 ve x = 1'dir. İşaret tablosunu gösterelim.
1 2
x -∞ x 1 x 2 +∞
a'nın a'nın a'nın x -∞ 1 2 +∞
2
ax + bx + c= 0 işaretiyle işaretinin işaretiyle
2
aynı tersi aynı x - 3x + 2 + - +
Q İşaret tablosunun en sağındaki a'nın işaretiyle aynıdır.
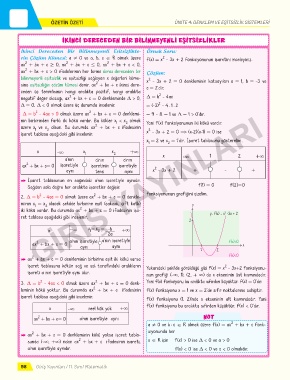
Sağdan sola doğru her aralıkta işaretler değişir. f(1) = 0 f(2)=0
2
2
2. ∆ = b - 4ac = 0 olmak üzere ax + bx + c = 0 denkle- fonksiyonunun grafiğini çizelim.
minin x = x olacak şekilde birbirine eşit (çakışık, çift katlı) y
1 2
2
iki kökü vardır. Bu durumda ax + bx + c = 0 ifadesinin işa- y= f(x) = x -3x + 2
2
ret tablosu aşağıdaki gibi incelenir.
2
x -∞ x = x = -b +∞
1 2
2a
2
ax + bx + c = 0 a'nın işaretiyle a'nın işaretiyle f(x)>0 x
aynı aynı
1 2
2
Q ax + bx + c = 0 denkleminin birbirine eşit iki kökü varsa f(x)<0
işaret tablosuna kökün sağ ve sol tarafındaki aralıkların Yukarıdaki şekilde görüldüğü gibi f(x) = x - 3x+2 fonksiyonu-
2
işareti a nın işaretiyle aynı olur.
nun grafiği (-∞, 1), (2, + ∞) da x ekseninin üst kısmındadır.
2
2
3. ∆ = b - 4ac < 0 olmak üzere ax + bx + c = 0 denk- Yani f(x) fonksiyonu bu aralıkta sıfırdan büyüktür. f(x) = 0'dır.
2
leminin kökü yoktur. Bu durumda ax + bx + c ifadesinin f(x) fonksiyonu x = 1 ve x = 2'de sıfır noktalarına sahiptir.
işaret tablosu aşağıdaki gibi incelenir. f(x) fonksiyonu (1, 2)'nda x ekseninin alt kısmındadır. Yani
x -∞ reel kök yok +∞ f(x) fonksiyonu bu aralıkta sıfırdan küçüktür. f(x) < 0'dır.
2
ax + bx + c= 0 a'nın işaretiyle aynı NOT
.
2
a  0 ve b c ∈ R olmak üzere f(x) = ax + bx + c fonk-
2
Q ax + bx + c = 0 denkleminin kökü yoksa işaret tablo- siyonunda her
2
sunda (-∞, +∞) ndan ax + bx + c ifadesinin işareti, x ∈ R için f(x) > 0 ise ∆ < 0 ve a > 0
a'nın işaretiyle aynıdır. f(x) < 0 ise ∆ < 0 ve a < 0 olmalıdır.
98 Giriş Yayınları / 11. Sınıf Matematik