Page 22 - 10. SINIF MATEMATİK DEFTERİM - GİRİŞ YAYINLARI

ÖZETİN ÖZETİ 6. ÜNİTE: UZAY GEOMETRİ

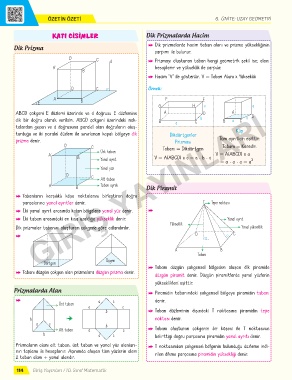
KATI CİSİMLER Dik Prizmalarda Hacim

Dik Prizma Q Dik prizmalarda hacim taban alanı ve prizma yüksekliğinin
çarpımı ile bulunur.
D' C' d Q Prizmayı oluşturan taban hangi geometrik şekil ise; alanı
A' hesaplanır ve yükseklik ile çarpılır.
B'
Q Hacim "V" ile gösterilir. V = Taban Alanı x Yükseklik

D C Örnek: A
A F E
E B
G H c a
ABCD çokgeni E düzlemi üzerinde ve d doğrusu E düzlemine A D A D
dik bir doğru olarak verilsin. ABCD çokgeni üzerindeki nok- B a C b B a C a
talardan geçen ve d doğrusuna paralel olan doğruların oluş-
turduğu ve iki paralel düzlem ile sınırlanan kapalı bölgeye dik Dikdörtgenler Küp
prizma denir. Prizması Tüm ayrıtları eşittir.
D' C' Tabanı = Dikdörtgen Tabanı = Karedir.
Üst taban
A' V = A(ABCD) x a
.
.
B' Yanal ayrıt V = A(ABCD) x c = a b c = a a a = a 3
.
.
Yanal yüz
D Ş YAYINLARI
C
Alt taban
A B Taban ayrıtı Dik Piramit
Q Tabanların karşılıklı köşe noktalarını birleştiren doğru
parçalarına yanal ayrıtlar denir. T Tepe noktası
GİRİ A Taban B
Q İki yanal ayrıt arasında kalan bölgelere yanal yüz denir. Q
Q İki taban arasındaki en kısa uzaklığa yükseklik denir. Yanal ayrıt
Dik prizmalar tabanını oluşturan çokgene göre adlandırılır. Yükseklik Yanal yükseklik
Q D C

Üçgen
Dörtgen
Q Tabanı düzgün çokgen olan prizmalara düzgün prizma denir. Q Tabanı düzgün çokgensel bölgeden oluşan dik piramide
düzgün piramit denir. Düzgün piramitlerde yanal yüzlerin
yükseklikleri eşittir.
Prizmalarda Alan Q Piramidin tabanındaki çokgensel bölgeye piramidin tabanı

Q a c denir.
Üst taban
a c
b Q Taban düzleminin dışındaki T noktasına piramidin tepe
h noktası denir.
a c b
Alt taban a c Q Tabanı oluşturan çokgenin bir köşesi ile T noktasının
b a c belirttiği doğru parçasına piramidin yanal ayrıtı denir.

Prizmaların alanı alt taban, üst taban ve yanal yüz alanları- Q T noktasından çokgensel bölgenin bulunduğu düzleme indi-
nın toplamı ile hesaplanır. Açınımda oluşan tüm yüzlerin alanı
2 taban alanı + yanal alandır. rilen dikme parçasına piramidin yüksekliği denir.

114 Giriş Yayınları / 10. Sınıf Matematik